
【題目】服裝店準備購進甲乙兩種服裝共100件,費用不得超過7500元.甲種服裝每件進價80元,每件售價120元;乙種服裝每件進價60元,每件售價90元.
(Ⅰ)設購進甲種服裝![]() 件,試填寫下表.
件,試填寫下表.
表一
購進甲種服裝的數量/件 | 10 | 20 | … |
|
購進甲種服裝所用費用/元 | 800 | 1600 | … | |
購進乙種服裝所用費用/元 | 5400 | … |
表二
購進甲種服裝的數量/件 | 10 | 20 | … |
|
甲種服裝獲得的利潤/元 | 800 | … | ||
乙種服裝獲得的利潤/元 | 2700 | 2400 | … |
(Ⅱ)給出能夠獲得最大利潤的進貨方案,并說明理由.
【答案】(Ⅰ)![]() ,4800,
,4800,![]() ,400,
,400,![]() ,
,![]() ;(Ⅱ)購進甲種服裝75件,乙種服裝25件時,可獲得最大利潤,理由見解析
;(Ⅱ)購進甲種服裝75件,乙種服裝25件時,可獲得最大利潤,理由見解析
【解析】
(1)甲服裝的件數乘以進貨價即為購進甲種服裝所用費用,乙的進貨價乘以(100-甲的件數)即為購進乙種服裝所用費用;利潤=(售價-進貨價)×件數;
(2)設購進甲種服裝![]() 件,根據費用不得超過7500元,求出x的范圍,然后求出利潤關于x的函數關系式,再由函數的性質求出最值即可.
件,根據費用不得超過7500元,求出x的范圍,然后求出利潤關于x的函數關系式,再由函數的性質求出最值即可.
(Ⅰ)表一
購進甲種服裝的數量/件 | 10 | 20 | … |
|
購進甲種服裝所用費用/元 | 800 | 1600 | … |
|
購進乙種服裝所用費用/元 | 5400 | 4800 | … |
|
表二
購進甲種服裝的數量/件 | 10 | 20 | … |
|
甲種服裝獲得的利潤/元 | 400 | 800 | … |
|
乙種服裝獲得的利潤/元 | 2700 | 2400 | … |
|
(Ⅱ)設購進甲種服裝![]() 件,由題意可知:
件,由題意可知:
![]()
解得:![]() .
.
購進甲種服裝![]() 件,總利潤為
件,總利潤為![]() 元,
元,![]() ,
,
![]() ,
,
∵![]() ,
,![]() 隨
隨![]() 的增大而增大,
的增大而增大,
∴當![]() 時,
時,![]() 有最大值,
有最大值,
則購進甲種服裝75件,乙種服裝25件時,可獲得最大利潤.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】對于下列說法,錯誤的個數是( )
①![]() 是分式;②當x≠1時,
是分式;②當x≠1時,![]() 成立;③當x=﹣3時,分式
成立;③當x=﹣3時,分式![]() 的值是零;④a
的值是零;④a![]() ;⑤
;⑤![]() ;⑥2﹣x
;⑥2﹣x![]() .
.
A.6個B.5個C.4個D.3個
查看答案和解析>>
科目:初中數學 來源: 題型:
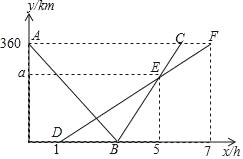
【題目】快、慢兩車分別從相距360km的佳市、哈市兩地出發,勻速行駛,先相向而行,慢車在快車出發1h后出發,到達佳市后停止行駛,快車到達哈市后,立即按原路原速返回佳市(快車調頭的時間忽略不計),快、慢兩車距哈市的路程y1(單位:km),y2(單位:km)與快車出發時間x(單位:h)之間的函數圖象如圖所示,請結合圖象信息解答下列問題:
(1)直接寫出慢車的行駛速度和a的值;
(2)快車與慢車第一次相遇時,距離佳市的路程是多少千米?
(3)快車出發多少小時后兩車相距為100km?請直接寫出答案.
查看答案和解析>>
科目:初中數學 來源: 題型:
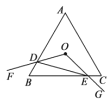
【題目】如圖,等邊三角形![]() 的邊長為4,點
的邊長為4,點![]() 是△
是△![]() 的中心,
的中心,![]() .繞點
.繞點![]() 旋轉
旋轉![]() ,分別交線段
,分別交線段![]() 于
于![]() 兩點,連接
兩點,連接![]() ,給出下列四個結論:①
,給出下列四個結論:①![]() ;②
;②![]() ;③四邊形
;③四邊形![]() 的面積始終等于
的面積始終等于![]() ;④△
;④△![]() 周長的最小值為6,上述結論中正確的個數是( )
周長的最小值為6,上述結論中正確的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝公司試銷一種成本為每件50元的![]() 恤衫.試銷中發現,當銷售單價是60元時,售出400件;銷售單價每降低1元,多售出10件.設試銷中銷售單價
恤衫.試銷中發現,當銷售單價是60元時,售出400件;銷售單價每降低1元,多售出10件.設試銷中銷售單價![]() (元)時的銷售量為
(元)時的銷售量為![]() (件).
(件).
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)設該公司獲得的總利潤為![]() 元,求
元,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)若要銷量不低于200件,且獲利至少5250元,則售價應在何范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是平行四邊形,CD為⊙O的切線,點C是切點.
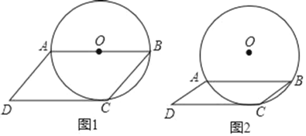
(1)如圖1,若AB為⊙O直徑,求四邊形ABCD各內角的度數;
(2)如圖2,若AB為弦,⊙O的半徑為3cm,當BC=2cm時,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形紙片ABCD,AB=7,BC=4,在矩形邊上有一點P,且DP=3.將矩形紙片折疊,使點B與點P重合,折痕所在直線交矩形兩邊于點E、F,則EF=__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,學校的實驗樓對面是一幢教學樓,小敏在實驗樓的窗口C處測得教學樓頂部D處的仰角為18°,教學樓底部B處的俯角為20°,教學樓的高BD=21m,求實驗樓與教學樓之間的距離AB(結果保留整數).(參考數據:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,以點O為圓心的圓分別交x軸的正半軸于點M,交y軸的正半軸于點N.劣弧![]() 的長為
的長為![]() ,直線
,直線![]() 與x軸、y軸分別交于點A、B.
與x軸、y軸分別交于點A、B.
(1)求證:直線AB與⊙O相切;
(2)求圖中所示的陰影部分的面積(結果用π表示)
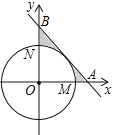
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com