
【題目】已知在△ABC中,AB=AC,AD⊥BC,垂足為點D,以AD為對角線作正方形AEDF,DE交AB于點M,DF交AC于點N,連結EF,EF分別交AB、AD、AC于點G、點O、點H.
(1)求證:EG=HF;
(2)當∠BAC=60°時,求![]() 的值;
的值;
(3)設![]() ,△AEH和四邊形EDNH的面積分別為S1和S2,求
,△AEH和四邊形EDNH的面積分別為S1和S2,求![]() 的最大值.
的最大值.

【答案】(1)見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據等腰三角形的判定與性質,正方形的性質易證△AGH為等腰三角形,通過“三線合一”可得OG=OH,即可得證;
(2)由等邊三角形的性質可設OH=a,則OA=OE=OF=![]() a,則EH=(
a,則EH=(![]() )a,HF=(
)a,HF=(![]() )a,
)a,
根據相似三角形判定易證△AEH∽△NFH,△AOH∽△ADC,△HNF∽△CND,然后通過相似三角形的對應邊成比整理即可得解;
(3)設EH=2m,則FH=2km,OA=![]() EF=(k+1)m,分別得到S1、S△HNF和S△EDF關于k,m的表達式,再根據S2=S△EDF - S△HNF得到S2的表達式,進而得到
EF=(k+1)m,分別得到S1、S△HNF和S△EDF關于k,m的表達式,再根據S2=S△EDF - S△HNF得到S2的表達式,進而得到![]() 關于k的表達式,通過配方法即可得解.
關于k的表達式,通過配方法即可得解.
(1)在正方形AEDF中,OE=OF,EF⊥AD,
∵AD⊥BC,
∴EF∥BC,
∴∠AGH=∠B,∠AHG=∠C,
而AB=AC,
∴∠B=∠C,
∴∠AGH=∠AHG,
∴AG=AH,
∴OG=OH,
∴OE-OG=OF-OH,
∴EG=FH;
(2)當∠BAC=60°時,△ABC為正三角形,
∵AD⊥EF,
∴∠OAH=30°,
∴![]() ,
,
設OH=a,則OA=OE=OF=![]() a,
a,
∴EH=(![]() )a,HF=(
)a,HF=(![]() )a,
)a,
∵AE∥FN,
∴△AEH∽△NFH,
∴![]() ,
,
∵EF∥BC,
∴△AOH∽△ADC,
∴![]() ,
,
∴CD=2a,
易證△HNF∽△CND,
∴![]() ,
,
∴![]() ;
;
(3)設EH=2m,則FH=2km,OA=![]() EF=(k+1)m,
EF=(k+1)m,
∴S1=(k+1)m2,
由(2)得,△AEH∽△NFH,
∴S△HNF=k2S1=k2(k+1)m2,
∴S2=S△EDF - S△HNF =(k+1)2m2 -k2(k+1)m2=(-k2+k+1)(k+1)m2,
∴![]() =-k2+k+1,
=-k2+k+1,
∴當k=![]() 時,
時,![]() 最大=
最大=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖是將一正方體貨物沿坡面AB裝進汽車貨廂的平面示意圖.已知長方體貨廂的高度BC為![]() 米,tanA=
米,tanA=![]() .現把圖中的貨物繼續往前平移,當貨物頂點D與C重合時,仍可把貨物放平裝進貨廂,求BD的長.(結果保留根號)
.現把圖中的貨物繼續往前平移,當貨物頂點D與C重合時,仍可把貨物放平裝進貨廂,求BD的長.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,點D是線段BC上一動點,連接AD,以AD為邊作△ADE∽△ABC,點N是AC的中點,連接NE,當線段NE最短時,線段CD的長為_____.
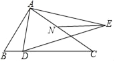
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家生產一種新型電子產品,制造時每件的成本為40元,通過試銷發現,銷售量![]() 萬件
萬件![]() 與銷售單價
與銷售單價![]() 元
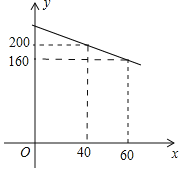
元![]() 之間符合一次函數關系,其圖象如圖所示.
之間符合一次函數關系,其圖象如圖所示.
![]() 求y與x的函數關系式;
求y與x的函數關系式;
![]() 物價部門規定:這種電子產品銷售單價不得超過每件80元,那么,當銷售單價x定為每件多少元時,廠家每月獲得的利潤
物價部門規定:這種電子產品銷售單價不得超過每件80元,那么,當銷售單價x定為每件多少元時,廠家每月獲得的利潤![]() 最大?最大利潤是多少?
最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了滿足學生的個性化需求,新課程改革已經勢在必行,某校積極開展拓展性課程建設,大體分為學科、文體、德育、其他等四個框架進行拓展課程設計。為了了解學生喜歡的拓展課程類型,學校隨機抽取了部分學生進行調查,調查后將數據繪制成扇形統計圖和條形統計圖(未繪制完整).

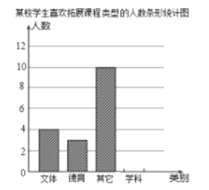
(1)求調查的學生總人數,并把條形圖補充完整并填寫扇形圖中缺失的數據;
(2)小明同學說:“因為調查的同學中喜歡文體類拓展課程的同學占16%,而喜歡德育類拓展課程的同學僅占12%,所以全校2000名學生中,喜歡文體類拓展課程的同學人數一定比喜歡德育類拓展課程的同學人數多。”你覺得小明說得對嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的直徑AB=6,AM,BN是⊙O的兩條切線,點D是AM上一點,連接OD,作BE∥OD交⊙O于點E,連接DE并延長交BN于點.
(1)求證:DC是⊙O的切線;
(2)設AD=x,BC=y.求y與x的函數關系式(不要求寫出自變量的取值范圍)
(3)若AD=1,連接AE并延長交BC于F,求EF的長.
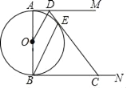
查看答案和解析>>
科目:初中數學 來源: 題型:
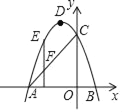
【題目】如圖,在直角坐標系中,拋物線y=﹣(x+1)2+4與x軸交于點A、B,與y軸交于點C.
(1)寫出拋物線頂點D的坐標 ;
(2)點D1是點D關于y軸的對稱點,判斷點D1是否在直線AC上,并說明理由;
(3)若點E是拋物線上的點,且在直線AC的上方,過點E作EF⊥x軸交線段AC于點F,求線段EF的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
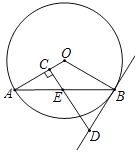
【題目】如圖,AB是⊙O的弦,過AB的中點E作EC⊥OA,垂足為C,過點B作直線BD交CE的延長線于點D,使得DB=DE.
(1)求證:BD是⊙O的切線;
(2)若AB=12,DB=5,求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D、E、F分別是邊AB、AC、BC的中點,要判定四邊形DBFE是菱形,下列所添加條件不正確的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com