
| PG |
| PC |
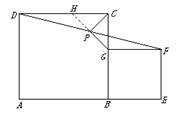
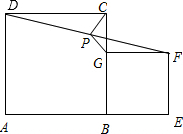 交DC于點H,構造全等三角形,經過推理使問題得到解決.
交DC于點H,構造全等三角形,經過推理使問題得到解決.| PG |
| PC |
 解:(1)如圖1,當點A,B,E在同一條直線上時,有結論:PG⊥PC,PG=PC.
解:(1)如圖1,當點A,B,E在同一條直線上時,有結論:PG⊥PC,PG=PC.


科目:初中數學 來源: 題型:閱讀理解
 25、請閱讀下列材料:
25、請閱讀下列材料:查看答案和解析>>
科目:初中數學 來源:2013屆江蘇省南京市鼓樓區中考二模數學試卷(帶解析) 題型:解答題
閱讀:
如圖①,已知:正方形ABCD,面積為a,點E、F、G、H分別是AB、BC、CD、DA邊的中點,連接AG、BH、CE、DF,求四邊形MNPQ的面積.


小明提出了如下的解決辦法:如圖②,分別將△AMH、△BNE、△CPF、△DQG分割并拼補成一個與正方形ABCD面積相等的新圖形.
請你參考小明同學解決問題的方法,利用圖形變換解決下列問題:
如圖③,在正方形ABCD中,E1、E2、E3、E4分別為AB、BC、CA、DA的中點,P 1、P2, Q1、Q2,M 1、M2,N1、N2分別為AB、BC、CA、DA的三等分點.
(1)在圖③中畫出一個和正方形ABCD面積相等的新圖形,并用陰影表示(保留畫圖痕跡);
(2)圖③中四邊形P4Q4M4N4的面積為 .
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省南京市鼓樓區中考二模數學試卷(解析版) 題型:解答題
閱讀:
如圖①,已知:正方形ABCD,面積為a,點E、F、G、H分別是AB、BC、CD、DA邊的中點,連接AG、BH、CE、DF,求四邊形MNPQ的面積.

小明提出了如下的解決辦法:如圖②,分別將△AMH、△BNE、△CPF、△DQG分割并拼補成一個與正方形ABCD面積相等的新圖形.
請你參考小明同學解決問題的方法,利用圖形變換解決下列問題:
如圖③,在正方形ABCD中,E1、E2、E3、E4分別為AB、BC、CA、DA的中點,P 1、P2, Q1、Q2,M 1、M2,N1、N2分別為AB、BC、CA、DA的三等分點.
(1)在圖③中畫出一個和正方形ABCD面積相等的新圖形,并用陰影表示(保留畫圖痕跡);
(2)圖③中四邊形P4Q4M4N4的面積為 .
查看答案和解析>>
科目:初中數學 來源:2013屆浙江省九年級第二學期期中考試數學試卷(解析版) 題型:解答題
【問題】如圖,在正方形ABCD內有一點P,PA= ,PB=
,PB= ,PC=1,求∠BPC的度數.
,PC=1,求∠BPC的度數.
分析根據已知條件比較分散的特點,我們可以通過旋轉變換將分散的已知條件集中在一起,于是將△BPC繞點B逆時針旋轉90°,得到了△BP′A(如圖),然后連結PP′.
解決問題請你通過計算求出圖17-2中∠BPC的度數;
【類比研究】如圖,若在正六邊形ABCDEF內有一點P,且PA= ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度數為 ;(2)直接寫出正六邊形ABCDEF的邊長為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com