
【題目】如圖,在Rt△ABC中,∠C=90,AC=6,BC=8,動點P從點A開始,沿邊AC向點C以每秒1個單位長度的速度運動,動點D從點A開始,沿邊AB向點B以每秒![]() 個單位長度的速度運動,且恰好能始終保持連結兩動點的直線PD⊥AC,動點Q從點C開始,沿邊CB向點B以每秒2個單位長度的速度運動,連結PQ.點P,D,Q分別從點A,C同時出發,當其中一點到達端點時,另兩個點也隨之停止運動,設運動時間為t秒(t≥0).
個單位長度的速度運動,且恰好能始終保持連結兩動點的直線PD⊥AC,動點Q從點C開始,沿邊CB向點B以每秒2個單位長度的速度運動,連結PQ.點P,D,Q分別從點A,C同時出發,當其中一點到達端點時,另兩個點也隨之停止運動,設運動時間為t秒(t≥0).
(1)當t為何值時,四邊形BQPD的面積為△ABC面積的![]() ?
?
(2)是否存在t的值,使四邊形PDBQ為平行四邊形?若存在,求出t的值;若不存在,說明理由;
(3)是否存在t的值,使四邊形PDBQ為菱形?若存在,求出t的值;若不存在,說明理由,并探究如何改變點Q的速度(勻速運動),使四邊形PDBQ在某一時刻為菱形,求點Q的速度。

【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)不存在;當點Q的速度為每秒
;(3)不存在;當點Q的速度為每秒![]() 個單位長度時,經過
個單位長度時,經過![]() 秒,四邊形PDBQ是菱形.
秒,四邊形PDBQ是菱形.
【解析】
(1)首先表示出四邊形面積以及求出三角形面積,列方程求解即可;
(2)由BQ//DP,可得當BQ=DP時,四邊形PDBQ是平行四邊形,由此可得關于t的方程,解方程即可得;
(3)利用(2)中所求,即可求得此時DP與BD的長,由DP≠BD,可判定平行四邊形PDBQ不能為菱形,然后設點Q的速度為每秒v個單位長度,由要使四邊形PDBQ為菱形,則PD=BD=BQ,列方程求解即可.
(1)∵直線PD⊥AC,
∴∠APD=90°,
又∵∠C=90°,
∴∠C=∠APD,
∴PD//BC,
在Rt△APD中,AD=![]() ,AP=t,
,AP=t,
∴PD=![]() ,PC=AC-AP=6-t,
,PC=AC-AP=6-t,
∵CQ=2t,BC=8,
∴BQ=8-2t,
∴四邊形BQPD的面積為:![]() (BQ+DP)×PC=
(BQ+DP)×PC=![]() (8-2t+
(8-2t+![]() t)(6-t),
t)(6-t),
△ABC的面積為:![]() ACBC=
ACBC=![]() ×6×8=24,
×6×8=24,
∴四邊形BQPD的面積為△ABC面積的![]() 時,
時,![]() ×24=
×24=![]() (8-2t+
(8-2t+![]() t)(6-t),
t)(6-t),
解得:![]() ,
,
∵當其中一點到達端點時,另兩個點也隨之停止運動,
∴t≤4,
∴![]() 不合題意,舍去,
不合題意,舍去,
∴當t為![]() 時,四邊形BQPD的面積為△ABC面積的
時,四邊形BQPD的面積為△ABC面積的![]() ;
;
(2)存在,
∵PD//BC,
∴BQ//DP,
∴當BQ=DP時,四邊形PDBQ是行四邊形,
即8-2t=![]() ,解得:t=
,解得:t=![]() ,
,
∴存在,t=![]() 時,四邊形PDBQ為平行四邊形;
時,四邊形PDBQ為平行四邊形;
(3)不存在,理由如下:
當![]() 時,
時,![]() ,
,
∴DP≠BD,
∴平行四邊形PDBQ不能為菱形;
設點Q的速度為每秒v個單位長度,
則BQ=8-vt,PD=![]() ,BD=10-
,BD=10-![]() ,
,
要使四邊形PDBQ成為菱形,則PD=BD=BQ,
當PD=BD時,即![]() ,解得:t=
,解得:t=![]() ,
,
當PD=BQ,t=![]() 時,即
時,即![]() ,解得:v=
,解得:v=![]() ,
,
所以當點Q的速度為每秒![]() 個單位長度時,經過
個單位長度時,經過![]() 秒,四邊形PDBQ是菱形.
秒,四邊形PDBQ是菱形.


科目:初中數學 來源: 題型:
【題目】已知A(n,-2),B(1,4)是一次函數y=kx+b的圖象和反比例函數y=![]() 的圖象的兩個交點,直線AB與y軸交于點C.
的圖象的兩個交點,直線AB與y軸交于點C.
(1)求反比例函數和一次函數的關系式;
(2)求△AOC的面積;
(3)求不等式kx+b-![]() <0的解集(直接寫出答案).
<0的解集(直接寫出答案).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場在春節期間搞優惠促銷活動,商場將29英寸和25英寸彩電共96臺分別以8折和7折出售,共得168400元。已知29英寸彩電原價為3000元/臺,25英寸彩電原價為2000元/臺,出售29英寸和25英寸彩電各多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以圓O為圓心,半徑為1的弧交坐標軸于A,B兩點,P是弧![]() 上一點(不與A,B重合),連接OP,設∠POB=α,則點P的坐標是
上一點(不與A,B重合),連接OP,設∠POB=α,則點P的坐標是

A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)操作發現:
如圖,在矩形ABCD中,E是BC的中點,將△ABE沿AE折疊后得到△AFE,點F在矩形ABCD內部,延長AF交CD于點G.猜想線段GF與GC有何數量關系?并證明你的結論.

(2)類比探究:
如圖,將(1)中的矩形ABCD改為平行四邊形,其它條件不變,(1)中的結論是否仍然成立?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知平行四邊形ABCD頂點A的坐標為(2,6),點B在y軸上,且AD∥BC∥x軸,過B,C,D三點的拋物線y=ax2+bx+c(a≠0)的頂點坐標為(2,2),點F(m,6)是線段AD上一動點,直線OF交BC于點E.
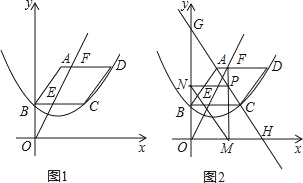
(1)求拋物線的表達式;
(2)設四邊形ABEF的面積為S,請求出S與m的函數關系式,并寫出自變量m的取值范圍;
(3)如圖2,過點F作FM⊥x軸,垂足為M,交直線AC于P,過點P作PN⊥y軸,垂足為N,連接MN,直線AC分別交x軸,y軸于點H,G,試求線段MN的最小值,并直接寫出此時m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是∠BAC的平分線,AD的垂線平分線交AB于點F,交BC的延長線于點E,連接AE,DF.
求證:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.
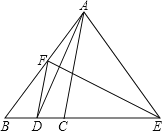
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工藝廠設計了一款成本為10元/件的工藝品投放市場進行試銷.
經過調查,得到如下數據:
銷售單價x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
每天銷售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(1)把上表中x、y的各組對應值作為點的坐標,在下面的平面直角坐標系中描出相應的點,猜想y與x的函數關系式,并求出函數關系式.
(2)物價部門規定,該工藝品的銷售單價最高不超過45元/件,當銷售單價x定為多少時,工藝廠試銷該工藝品每天獲得的利潤8000元?(利潤=銷售總價﹣成本總價)
(3)當銷售單價定為多少時,工藝廠試銷該工藝品每天獲得的利潤最大?最大利潤是多少?(利潤=銷售總價﹣成本總價)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com