
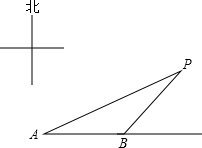
 已知:如圖,為了躲避海盜,一輪船一直由西向東航行,早上8點,在A處測得小島P的方向是北偏東75°,以每小時15海里的速度繼續向東航行,10點到達B處,并測得小島P的方向是北偏東60°,若小島周圍25海里內有暗礁,問該輪船是否能一直向東航行?
已知:如圖,為了躲避海盜,一輪船一直由西向東航行,早上8點,在A處測得小島P的方向是北偏東75°,以每小時15海里的速度繼續向東航行,10點到達B處,并測得小島P的方向是北偏東60°,若小島周圍25海里內有暗礁,問該輪船是否能一直向東航行?
 BP=15海里<25海里
BP=15海里<25海里

 精英口算卡系列答案
精英口算卡系列答案科目:初中數學 來源: 題型:
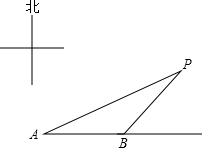 已知:如圖,為了躲避海盜,一輪船一直由西向東航行,早上8點,在A處測得小島P的方向是北偏東75°,以每小時15海里的速度繼續向東航行,10點到達B處,并測得小島P的方向是北偏東60°,若小島周圍25海里內有暗礁,問該輪船是否能一直向東航行?
已知:如圖,為了躲避海盜,一輪船一直由西向東航行,早上8點,在A處測得小島P的方向是北偏東75°,以每小時15海里的速度繼續向東航行,10點到達B處,并測得小島P的方向是北偏東60°,若小島周圍25海里內有暗礁,問該輪船是否能一直向東航行?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com