
【題目】如圖![]() ,矩形
,矩形![]() 的兩條邊
的兩條邊![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,已知點
軸上,已知點![]() 、點
、點![]() .
.
(1)若把矩形![]() 沿直線
沿直線![]() 折疊,使點
折疊,使點![]() 落在點
落在點![]() 處,直線
處,直線![]() 與
與![]() 的交點分別為
的交點分別為![]() ,求折痕
,求折痕![]() 的長;
的長;
(2)在(1)的條件下,點![]() 在
在![]() 軸上,在平面內是否存在點
軸上,在平面內是否存在點![]() ,使以
,使以![]() 為頂點的四邊形是菱形?若存在,則請求出點
為頂點的四邊形是菱形?若存在,則請求出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)如圖![]() ,若
,若![]() 為
為![]() 邊上的一動點,在
邊上的一動點,在![]() 上取一點
上取一點![]() ,將矩形
,將矩形![]() 繞點
繞點![]() 順時針旋轉一周,在旋轉的過程中,
順時針旋轉一周,在旋轉的過程中,![]() 的對應點為
的對應點為![]() ,請直接寫出
,請直接寫出![]() 的最大值和最小值.
的最大值和最小值.


【答案】(1)折痕![]() 的長為
的長為![]() ;(2)點
;(2)點![]() 坐標為
坐標為![]() 或
或![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 的最小值為
的最小值為![]() ,
,![]() 的最大值為5.
的最大值為5.
【解析】
(1)連接AD,根據(jù)矩形的性質可求出![]() ,繼而得
,繼而得![]() ,設
,設![]() ,則
,則![]() ,在
,在![]() 中,根據(jù)勾股定理求出DC長,繼而在
中,根據(jù)勾股定理求出DC長,繼而在![]() 中
中![]() 利用勾股定理求出DF長,證明
利用勾股定理求出DF長,證明![]() ,由全等三角形的性質得EF=DF,進而可求得答案;
,由全等三角形的性質得EF=DF,進而可求得答案;
(2)分兩咱情形分別討論即可:DE為菱形的邊;DE為菱形的對角線;
(3)由題意點M在如圖3中的圓環(huán)內或兩個圓上,利用圖象法即可解決問題.
(1)連接AD,

![]() 四邊形
四邊形![]() 是矩形,
是矩形,![]() ,
,
![]() ,
,
由折疊可得:![]() ,設
,設![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,即
,即![]() ,
,
在![]() 中
中![]() , 即
, 即![]() ,
,
解得![]() ,
,
![]() 四邊形
四邊形![]() 是矩形,
是矩形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 折痕
折痕![]() 的長為
的長為![]() ;
;
(2)由(1)可知,![]() ,
,
①當![]() 為菱形的邊時,
為菱形的邊時,![]() ,可得
,可得![]() ,
,
②當![]() 為菱形的對角線時,
為菱形的對角線時,![]() 與
與![]() 重合,
重合,![]() 與
與![]() 重合,
重合,![]() ,
,
③當點![]() 在第三象限,
在第三象限,![]() 與
與![]() 關于
關于![]() 軸對稱,
軸對稱,![]() ,
,
綜上所述,點![]() 坐標為
坐標為![]() 或
或![]() 或
或![]() 或
或![]() ;
;
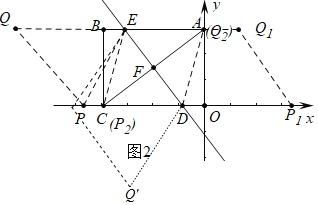
(3)如圖![]() 中,作
中,作![]() 則
則![]() ,
,

觀察圖形可知,![]() 的最小值
的最小值![]()
![]() ,
,
![]() 的最大值
的最大值![]()
![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】已知如圖,在平面直角坐標系xOy中,點A、B、C分別為坐標軸上上的三個點,且OA=1,OB=3,OC=4,
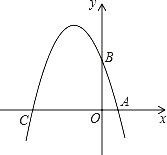
(1)求經(jīng)過A、B、C三點的拋物線的解析式;
(2)在平面直角坐標系xOy中是否存在一點P,使得以以點A、B、C、P為頂點的四邊形為菱形?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)若點M為該拋物線上一動點,在(2)的條件下,請求出當|PM﹣AM|的最大值時點M的坐標,并直接寫出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c(a≠0)的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸相交于點C(0,﹣3)
(1)求該二次函數(shù)的解析式;
(2)設E是y軸右側拋物線上異于點A的一個動點,過點E作x軸的平行線交拋物線于另一點F,過點F作FG垂直于x軸于點G,再過點E作EH垂直于x軸于點H,得到矩形EFGH,則在點E的運動過程中,當矩形EFGH為正方形時,求出該正方形的邊長;
(3)設P點是x軸下方的拋物線上的一個動點,連接PA、PC,求△PAC面積的取值范圍,若△PAC面積為整數(shù)時,這樣的△PAC有幾個?
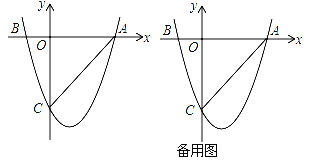
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校公布了該校反映各年級學生體育達標情況的兩張統(tǒng)計圖,該校七、八、九三個年級共有學生800人。甲,乙,丙三個同學看了這兩張統(tǒng)計圖后,甲說:“七年級的體育達標率最高.”乙說:“八年級共有學生264人。”丙說:“九年級的體育達標率最高。”甲、乙、丙三個同學中,說法正確的是_____________。


查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在![]() 中,
中,![]() 分別是
分別是![]() 的中點,若等腰
的中點,若等腰![]() 繞點
繞點![]() 逆時針旋轉,得到等腰
逆時針旋轉,得到等腰![]() ,設旋轉角為
,設旋轉角為![]() ,記直線
,記直線![]() 與
與![]() 的交點為
的交點為![]()


(1)如圖![]() ,當
,當![]() 時,線段
時,線段![]() 的長等于 ,線段
的長等于 ,線段![]() 的長等于 .(直接填寫結果)
的長等于 .(直接填寫結果)
(2)如圖![]() ,當
,當![]() 時,求證:
時,求證:![]() ,且
,且![]() ;
;
(3)設![]() 的中點為
的中點為![]() ,則線段
,則線段![]() 的長為 (直接填寫結果).
的長為 (直接填寫結果).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:△ABC與△A'B'C在平面直角坐標系中的位置如圖.

(1)分別寫出B、B'的坐標:B______;B′______;
(2)若點P(a,b)是△ABC內部一點,則平移后△A'B'C內的對應點P′的坐標為______;
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我市建設森林城市需要大量的樹苗,某生態(tài)示范園負責對甲、乙、丙、丁四個品種的樹苗共500株進行樹苗成活率試驗,從中選擇成活率高的品種進行推廣.通過試驗得知:丙種樹苗的成活率為89.6%,把試驗數(shù)據(jù)繪制成下面兩幅統(tǒng)計圖.(部分信息未給出)
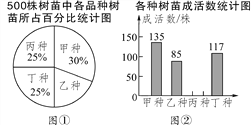
(1)試驗所用的乙種樹苗的數(shù)量是_______株;
(2)求出丙種樹苗的成活數(shù),并把圖②補充完整;
(3)你認為應選哪種樹苗進行推廣?請通過計算說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,如圖正方形
中,如圖正方形![]() 的頂點
的頂點![]() ,
,![]() 坐標分別為
坐標分別為![]() ,
,![]() ,點
,點![]() ,
,![]() 坐標分別為
坐標分別為![]() ,
,![]() ,且
,且![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() .設正方形
.設正方形![]() 與正方形
與正方形![]() 重疊部分面積為
重疊部分面積為![]() .
.

(1)①當點![]() 與點
與點![]() 重合時,
重合時,![]() 的值為______;②當點
的值為______;②當點![]() 與點
與點![]() 重合時,
重合時,![]() 的值為______.
的值為______.
(2)請用含![]() 的式子表示
的式子表示![]() ,并直接寫出
,并直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知![]() ,
, ![]() 是一次函數(shù)
是一次函數(shù)![]() 的圖象和反比例函數(shù)
的圖象和反比例函數(shù)![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1) 求一次函數(shù)、反比例函數(shù)的關系式;
(2) 求△AOB的面積.
(3) 當自變量x滿足什么條件時,y1>y2 .(直接寫出答案)
(4)將反比例函數(shù)![]() 的圖象向右平移n(n>0)個單位,得到的新圖象經(jīng)過點(3,-4),求對應的函數(shù)關系式y(tǒng)3.(直接寫出答案)
的圖象向右平移n(n>0)個單位,得到的新圖象經(jīng)過點(3,-4),求對應的函數(shù)關系式y(tǒng)3.(直接寫出答案)

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com