
 .
. ,求這時點D的坐標.
,求這時點D的坐標.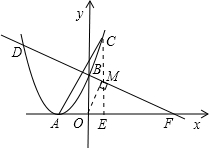
 ,
, ,
, ,
, ,
,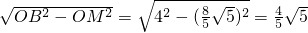 ;
;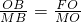 ,
,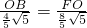 ,
, x+4;
x+4;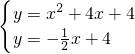 ,
,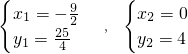 ,
,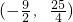 .
. ,進而可利用勾股定理求得BM的長;在△EOF中,OM⊥EF,易證得△OBM∽△FOM,根據相似三角形所得比例線段即可求得OF的長,也就得到了F點的坐標,進而可利用待定系數法求得直線BD的解析式,聯立拋物線的解析式即可求出點D的坐標.
,進而可利用勾股定理求得BM的長;在△EOF中,OM⊥EF,易證得△OBM∽△FOM,根據相似三角形所得比例線段即可求得OF的長,也就得到了F點的坐標,進而可利用待定系數法求得直線BD的解析式,聯立拋物線的解析式即可求出點D的坐標.

科目:初中數學 來源: 題型:
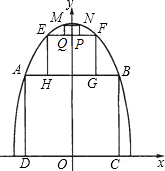 為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:
為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:查看答案和解析>>
科目:初中數學 來源: 題型:
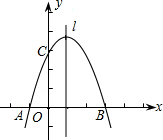 ,B,C三點的拋物的對稱軸為直線l,D為對稱軸l上一動點.
,B,C三點的拋物的對稱軸為直線l,D為對稱軸l上一動點.查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(32):2.3 二次函數的應用(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(52):2.8 二次函數的應用(解析版) 題型:解答題
 為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:
為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:查看答案和解析>>
科目:初中數學 來源:2005年浙江省杭州市中考數學試卷(解析版) 題型:解答題
 (2005•杭州)為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:
(2005•杭州)為了參加市科技節展覽,同學們制造了一個截面為拋物線形的隧道模型,用了三種正方形的鋼筋支架.在畫設計圖時,如果在直角坐標系中,拋物線的函數解析式為y=-x2+c,正方形ABCD的邊長和正方形EFGH的邊長之比為5:1,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com