
【題目】綜合題。
(1)計算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化簡,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并從﹣tan60°≤x≤2cos30°取出一個合適的整數,求出式子的值.
﹣x+1),并從﹣tan60°≤x≤2cos30°取出一個合適的整數,求出式子的值.
【答案】
(1)解:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]()
=1+2+2 ![]()
=3;
(2)解: ![]() ÷(
÷( ![]() ﹣x+1)
﹣x+1)
= ![]()
= ![]()
= ![]() ,
,
∵﹣tan60°≤x≤2cos30°
∴ ![]() ,
,
∴當x=1時,原式= ![]() =﹣1.
=﹣1.
【解析】(1)根據零指數冪、負整數指數冪、絕對值可以解答本題;(2)先化簡題目中的式子,然后根據﹣tan60°≤x≤2cos30°,從中選取使得原分式有意義的x的整數值代入即可解答本題.
【考點精析】認真審題,首先需要了解零指數冪法則(零次冪和負整數指數冪的意義: a0=1(a≠0);a-p=1/ap(a≠0,p為正整數)),還要掌握整數指數冪的運算性質(aman=am+n(m、n是正整數);(am)n=amn(m、n是正整數);(ab)n=anbn(n是正整數);am/an=am-n(a不等于0,m、n為正整數);(a/b)n=an/bn(n為正整數))的相關知識才是答題的關鍵.


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,拋物線y=ax2﹣x+3(a≠0)交x軸于A、B兩點,交y軸于點C,且對稱軸為直線x=﹣2.
(1)求該拋物線的解析式及頂點D的坐標;
(2)若點P(0,t)是y軸上的一個動點,請進行如下探究: 探究一:如圖1,設△PAD的面積為S,令W=tS,當0<t<4時,W是否有最大值?如果有,求出W的最大值和此時t的值;如果沒有,說明理由;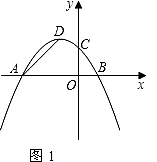
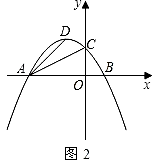
探究二:如圖2,是否存在以P、A、D為頂點的三角形與Rt△AOC相似?如果存在,求點P的坐標;如果不存在,請說明理由.(參考資料:拋物線y=ax2+bx+c(a≠0)對稱軸是直線x= ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A1、A2、A3、…、An(n為正整數)都在數軸上.點A2在點A1的左邊,且A1A2=1;點A3在點A2的右邊,且A2A3=2;點A4在點A3的左邊,且A3A4=3;…,點A2018在點A2017的左邊,且A2017A2018=2017,若點A2018所表示的數為2018,則點A1所表示的數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明受《烏鴉喝水》故事的啟發,利用量桶和體積相同的小球進行了如下操作:請根據圖中給出的信息,解答下列問題:
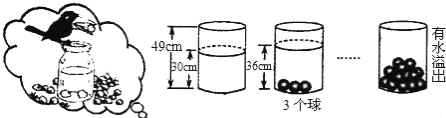
(1)放入一個小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)與小球個數x(個)之間的函數關系式;
(3)當量桶中水面上升至距離量桶頂部3cm時,應在量桶中放入幾個小球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一種新運算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代數式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】亞健康是時下社會熱門話題,進行體育鍛煉是遠離亞健康的一種重要方式,為了解某市初中學生每天進行體育鍛煉的時間情況,隨機抽樣調查了100名初中學生,根據調查結果得到如圖所示的統計圖表.
類別 | 時間t(小時) | 人數 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
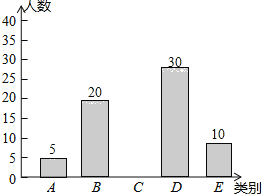
請根據圖表信息解答下列問題:
(1)a= ;
(2)補全條形統計圖;
(3)小王說:“我每天的鍛煉時間是調查所得數據的中位數”,問小王每天進行體育鍛煉的時間在什么范圍內?
(4)據了解該市大約有30萬名初中學生,請估計該市初中學生每天進行體育鍛煉時間在1小時以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】臨海市初中第三教研區為了豐富學生課余活動,組織同學開展每周一次的社團活動,活動內容有足球、跳繩、跳舞、籃球、象棋共5項,為方便組織,規定每位同學只能報一項活動,根據報名繪制了如下兩幅尚不完整的統計圖,解答下列問題: 
(1)將條形統計圖補充完整;
(2)寫出扇形統計圖中的m和n的值;
(3)瑤瑤和欣欣兩名同學對足球、籃球、象棋三項活動都很感興趣,決定從三項活動中隨機抽取一項參加,利用樹狀圖或列表表示所有可能結果,并求出兩人參加同一項目的概率;
(4)由于場地限制,參加足球活動的學生人數不能超過參加其余活動學生人數的 ![]() ,那么至少幾位同學需要從參加足球活動調整到參加其余活動?
,那么至少幾位同學需要從參加足球活動調整到參加其余活動?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地電話撥號上網有兩種收費方式,用戶可以任選其一:
(A)計時制,0.08元/分;
(B)包月制,50元/月(限一部個人住宅電話上網);
此外,每種上網方式都附加通信費0.02元/分.
(1)某用戶某月上網時間為x分鐘,則該用戶在A、B兩種收費方式下應支付費用各多少元?
(2)如果一個月內上網200分鐘和300分鐘,按兩種收費方式各需交費多少元?
(3)是否存在某一時間,會出現兩種收費方式一樣的情況?如果存在,請求出這時的上網時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,O是對角線AC與BD的交點,M是BC邊上的動點(點M不與B、C重合),過點C作CN垂直DM交AB于點N,連結OM、ON、MN.下列五個結論:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,則
;③ON⊥OM;④若AB=2,則![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正確結論是_________.(只填番號)
.其中正確結論是_________.(只填番號)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com