Question

【題目】請仔細閱讀下面材料，然后解決問題：

在分式中，對于只含有一個字母的分式，當分子的次數大于或等于分母的次數時，我們稱之為“假分式”．例如： ， ；當分子的次數小于分母的次數時，我們稱之為“真分式”，例如： ， ．我們知道，假分數可以化為帶分數，例如： ，類似的，假分式也可以化為“帶分式”（整式與真分式和的形式），例如： ．

（1）將分式化為帶分式；

（2）當x取哪些整數值時，分式的值也是整數？

（3）當x的值變化時，分式的最大值為　　．

【答案】（1）2+；（2）x=0，2，﹣2，4；（3）.

【解析】試題分析：（1）仿照閱讀材料中的方法加你個原式變形即可；

（2）原式變形后，根據結果為整數確定出整數x的值即可；

（3）原式變形后，確定出分式的最大值即可．

試題解析:（1）原式==2+；

（2）由（1）得： =2+，

要使為整數，則必為整數，

∴x﹣1為3的因數，

∴x﹣1=±1或±3，

解得：x=0，2，﹣2，4；

（3）原式==2+，

當x2=0時，原式取得最大值．

故答案為： .

【題型】解答題
【結束】
28

【題目】已知，△ABC中,AC＝BC,∠ACB＝90°，點P在射線AC上,連接PB,將線段PB繞點B逆時針旋轉90°得線段BN，AN交直線BC于M．

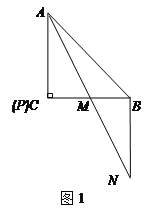
(1)圖1，若點P與點C重合，則＝______,＝______．(直接寫出結果)

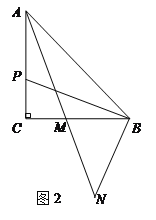
(2)圖2，若點P在線段AC上，求證: AP＝2MC；

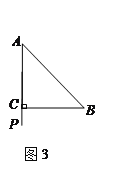
(3)圖3，若點P在線段AC的延長線上，完成圖形,并直接寫出 ＝______．

Answer 1

【答案】⑴1, ; ⑵證明見解析; (3)

【解析】試題分析：（1）先求出 再利用“角角邊”證明和 全等，根據全等三角形對應邊相等可得 再求出 然后求解即可；
（2）過點作于，根據同角的余角相等求出，然后利用“角角邊”證明和全等，根據全等三角形對應邊相等可得 然后求出 再利用“角角邊”證明和全等根據全等三角形對應邊相等可得 整理即可得證；
（3）過點作交的延長線于，然后與（2）的求解方法相同．

試題解析：⑴1；

(2)證明：如圖2，過點N作NE⊥BC于E，

∵線段PB繞點B逆時針旋轉得線段BN，

∴∠PBC=∠BNE，

在△PBC和△BNE中,

∴BE=PC，NE=BC，

∴AP=ACPC=BCBE=CE，AC=NE，

在△ACM和△NEM中,

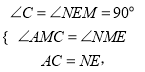
∴MC=ME，

∴CE=2MC，

∴AP=2MC；