
如圖,在▱ABCD中,E是AD上一點,連接BE,F為BE中點,且AF=BF,
(1)求證:四邊形ABCD為矩形;
(2)過點F作FG⊥BE,垂足為F,交BC于點G,若BE=BC,S△BFG=5,CD=4,求CG.

考點:
矩形的判定與性質;勾股定理;平行四邊形的性質.
分析:
(1)求出∠BAE=90°,根據矩形的判定推出即可;
(2)求出△BGE面積,根據三角形面積公式求出BG,得出EG長度,根據勾股定理求出GH,求出BE,得出BC長度,即可求出答案.
解答:
(1)證明:∵F為BE中點,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四邊形ABCD為平行四邊形,
∴四邊形ABCD為矩形;

(2)解:連接EG,過點E作EH⊥BC,垂足為H,
∵F為BE的中點,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10= BG•EH,
BG•EH,
∴BG=GE=5,
在Rt△EGH中,GH= =3,
=3,
在Rt△BEH中,BE= =4
=4 =BC,
=BC,
∴CG=BC﹣BG=4 ﹣5.
﹣5.
點評:
本題考查了矩形的判定,勾股定理,三角形的面積,線段垂直平分線性質等知識點的應用,主要考查學生綜合運用性質進行推理的能力,題目比較好,有一定的難度.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:
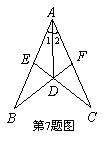
如圖,∠1=∠2,∠C=∠B,下列結論中不正確的是( )
A. △DAB≌△DAC B. △DEA≌△DFA C. CD=DE D. ∠AED=∠AFD
查看答案和解析>>
科目:初中數學 來源: 題型:
下列三角形中,是直角三角形的是( )
(A)三角形的三邊滿足關系a+b=c (B)三角形的三邊比為1∶2∶3
(C)三角形的一邊等于另一邊的一半 (D)三角形的三邊為9,40,41
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,正方形ABCD的邊長為2,點E、F分別為邊AD、BC上的點,EF= ,點G、H分別為AB、CD邊上的點,連接GH,若線段GH與EF的夾角為45°,則GH的長為( )
,點G、H分別為AB、CD邊上的點,連接GH,若線段GH與EF的夾角為45°,則GH的長為( )

|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖是置于水平地面上的一個球形儲油罐,小敏想測量它的半徑.
 在陽光下,他測得球的影子的最遠點A到球罐與地面接觸點B的
在陽光下,他測得球的影子的最遠點A到球罐與地面接觸點B的
距離是10米(如示意圖,AB=10米);同一時刻,他
又測得豎直立在地面上長為1米的竹竿的影子長為2
米,那么,球的半徑是 米.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com