
【題目】在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3![]() .分別以OA、OC邊所在直線為x軸、y軸建立如圖1所示的平面直角坐標系.
.分別以OA、OC邊所在直線為x軸、y軸建立如圖1所示的平面直角坐標系.
(1)求點B的坐標;
(2)已知D、E分別為線段OC、OB上的點,OD=5,OE=2EB,直線DE交x軸于點F,過點E作EG⊥x軸于G,且EG:OG=2.求直線DE的解析式;
(3)點M是(2)中直線DE上的一個動點,在x軸上方的平面內是否存在另一點N,使以O、D、M、N為頂點的四邊形是菱形?若存在,請求出點N的坐標;若不存在,請說明理由.

【答案】
【1】如圖,作BH⊥x軸,垂足為H,那么四邊形BCOH為矩形,OH=CB=3.
在Rt△ABH中,AH=3,BA=![]() ,所以BH=6.因此點B的坐標為(3,6).
,所以BH=6.因此點B的坐標為(3,6).
【2】因為OE=2EB,所以![]() ,
,![]() ,E(2,4).
,E(2,4).
設直線DE的解析式為y=kx+b,代入D(0,5),E(2,4),
得![]() 解得
解得![]() ,
,![]() .所以直線DE的解析式為
.所以直線DE的解析式為![]() .
.
【3】由![]() ,知直線DE與x軸交于點F(10,0),OF=10,DF=
,知直線DE與x軸交于點F(10,0),OF=10,DF=![]() .
.
①如圖,當DO為菱形的對角線時,MN與DO互相垂直平分,點M是DF的中點.
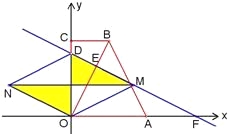
此時點M的坐標為(5,![]() ),點N的坐標為(-5,
),點N的坐標為(-5,![]() ).
).
②如圖,當DO、DN為菱形的鄰邊時,點N與點O關于點E對稱,此時點N的坐標為(4,8).
③如圖,當DO、DM為菱形的鄰邊時,NO=5,延長MN交x軸于P.
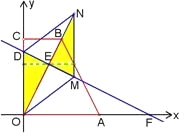
由△NPO∽△DOF,得![]() ,
,
即![]() .
.
解得![]() ,
,![]() .此時點N的坐標為
.此時點N的坐標為![]() .
.
【解析】
(1)作BH⊥x軸,構建矩形,在直角三角形中求得BH=6,從而求得點B的坐標為(3,6)。
(2)待定系數法求得直線解析式。
(3)綜合性較強,考慮全面是正確解題的關鍵。


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,點D為BC的中點,CE⊥AD于點E,其延長線交AB于點F,連接DF.求證:∠ADC=∠BDF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小亮分別從甲地和乙地同時出發,沿同一條路相向而行,小明開始跑步,中途改為步行,到達乙地恰好用![]() 小亮騎自行車以
小亮騎自行車以![]() 的速度直接到甲地,兩人離甲地的路程
的速度直接到甲地,兩人離甲地的路程![]() 與各自離開出發地的時間
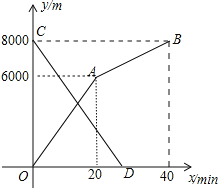
與各自離開出發地的時間![]() 之間的函數圖象如圖所示,
之間的函數圖象如圖所示,
![]() 甲、乙兩地之間的路程為______m,小明步行的速度為______
甲、乙兩地之間的路程為______m,小明步行的速度為______![]() ;
;
![]() 求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
![]() 求兩人相遇的時間.
求兩人相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
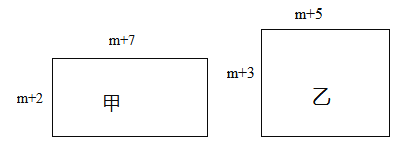
【題目】已知有甲、乙兩個長方形,它們的邊長如圖所示(m為正整數),面積分別為S1、S2.
(1)請比較S1與S2的大小: S1 S2;
(2)若一個正方形與甲的周長相等.
①求該正方形的邊長(用含m的代數式表示);
②若該正方形的面積為S3,試探究:S3與S1的差(即S3﹣S1)是否為常數?若為常數,求出這個常數;如果不是,請說明理由;
(3)若滿足條件0<n<|S1﹣S2|的整數n有且只有8個,直接寫出m的值并分別求出S1與S2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列一組圖形中點的個數,其中第1個圖中共有4個點,第2個圖中共有10個點,第3個圖中共有19個點,…,按此規律第100個圖中共有點的個數是
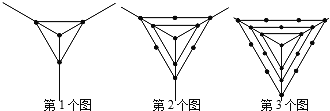
A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目:初中數學 來源: 題型:
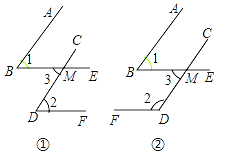
【題目】已知一個角的兩邊與另一個角的兩邊分別平行,請結合圖,探索這兩個角之間的關系,并說明理由.
(1)如圖①,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(2)如圖②,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(3)經過上述證明,我們可得出結論,如果一個角的兩邊與另一個角的兩邊分別平行,那么這兩個角 ;
(4)若這兩個角的兩邊分別平行,且一個角比另一個角的3倍少60°,則這兩個角分別是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x+2)(x2-4x+6)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.兩數和的完全平方公式 |
D.兩數差的完全平方公式 |
(2)該同學因式分解的結果是否徹底?________.(填“徹底”或“不徹底”)若不徹底,請直接寫出因式分解的最后結果_________ .
(3)請你模仿以上方法嘗試對多項式(x2-2x)(x2-2x+2)+1進行因式分解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①、②、③是三個可以自由轉動的轉盤.
(1)若同時轉動①、②兩個轉盤,則兩個轉盤停下時指針所指的數字都是2的概率為;
(2)甲、乙兩人用三個轉盤玩游戲,甲轉動轉盤,乙記錄指針停下時所指的數字.游戲規定:當指針所指的三個數字中有數字相同時,就算甲贏,否則就算乙贏.請判斷這個游戲是否公平,并說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com