
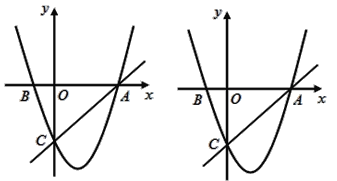
【題目】如圖,在平面直角坐標系中,已知拋物線y=x2+bx+c過A,B,C三點,點A的坐標是(3,0),點C的坐標是(0,-3),動點P在拋物線上.
(1)b =_________,c =_________,點B的坐標為_____________;(直接填寫結果)
(2)是否存在點P,使得△ACP是以AC為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由;
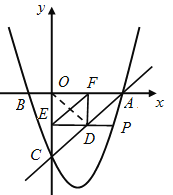
(3)過動點P作PE垂直y軸于點E,交直線AC于點D,過點D作x軸的垂線.垂足為F,連接EF,當線段EF的長度最短時,求出點P的坐標.
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)存在P的坐標是
(2)存在P的坐標是![]() 或
或![]() (3)當EF最短時,點P的坐標是:(
(3)當EF最短時,點P的坐標是:(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】試題分析:(1)根據題意得出答案;(2)分以點C為直角頂點和點A為直角頂點兩種情況分別進行計算;兩種情況都根據等腰直角三角形的性質得出點的坐標;(3)根據垂線段最短,可得當OD⊥AC時,OD最短,即EF最短,根據OC=OA=3,OD⊥AC得出 D是AC的中點,從而得出點P的縱坐標,然后根據題意得出方程,從而求出點P的坐標.
試題解析:(1)![]() ,
,![]() , (-1,0).
, (-1,0).
(2)存在.
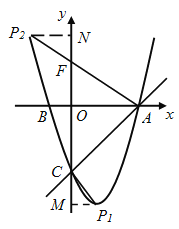
第一種情況,當以C為直角頂點時,過點C作CP1⊥AC,交拋物線于點P1.過點P1作y軸的垂線,垂足是M.
∵OA=OC,∠AOC =90° ∴∠OCA=∠OAC=45°. ∵∠ACP1=90°, ∴∠MCP1=90°-45°=45°=∠C P1M.
∴MC=MP1. 由(1)可得拋物線為![]() .
.
設![]() ,則
,則![]() , 解得:
, 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() . 則P1的坐標是
. 則P1的坐標是![]() .
.
第二種情況,當以A為直角頂點時,過點A作AP2⊥AC,交拋物線于點P2,過點P2作y軸的垂線,垂足是N,AP2交y軸于點F. ∴P2N∥x軸.由∠CAO=45°, ∴∠OAP2=45°. ∴∠FP2N=45°,AO=OF=3.
∴P2N=NF. 設![]() ,則
,則![]() . 解得:
. 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() , 則P2的坐標是
, 則P2的坐標是![]() .
.
綜上所述,P的坐標是![]() 或
或![]()
(3)連接OD,由題意可知,四邊形OFDE是矩形,則OD=EF.
根據垂線段最短,可得當OD⊥AC時,OD最短,即EF最短. 由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC, ∴ D是AC的中點. 又∵DF∥OC, ∴![]() .
.
∴點P的縱坐標是![]() 則
則![]() , 解得:
, 解得:![]() .
.
∴當EF最短時,點P的坐標是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ABC=90°.
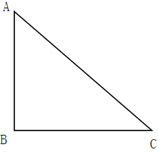
(1)請在BC上找一點P,作⊙P與AC,AB都相切,切點為Q;(尺規作圖,保留作圖痕跡)
(2)若AB=3,BC=4,求第(1)題中所作圓的半徑;
(3)連結BQ,第(2)中的條件均不變,求sin∠CBQ.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶統景溫泉風景區被喻為“巴渝十二景”.為豐富旅游配套資源,鎮政府決定大力發動農戶擴大柑橘和蔬菜種植面積,并取得了較好的經濟效益.今年該鎮柑橘和蔬菜的收成比去年增加了80噸,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,從而使今年的收成共達到了420噸.
(1)統景鎮去年柑橘和蔬菜的收成各是多少噸?
(2)由于今年大豐收,鎮政府計劃用甲、乙兩種貨車共33輛將柑橘和蔬菜一次性運去參加渝洽會.已知一輛甲種貨車最多可裝13噸柑橘和3噸蔬菜;一輛乙種貨車最多可裝柑橘5噸和蔬菜6噸,安排甲、乙兩種貨車共有幾種方案?
(3)若甲種貨車的運費為每輛600元,乙種貨車的運費為每輛500元,在(2)的情況下,如何安排運費最少,最少為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
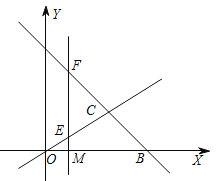
【題目】如圖,直線OC,BC的函數關系式分別是y1=![]() x和y2=-x+6,兩直線的交點為C.
x和y2=-x+6,兩直線的交點為C.
(1)求點C的坐標,并直接寫出y1>y2時x的范圍;
(2)在直線y1上找點D,使△DCB的面積是△COB的一半,求點D的坐標;
(3)點M(t,0)是![]() 軸上的任意一點,過點M作直線l⊥
軸上的任意一點,過點M作直線l⊥![]() 軸,分別交直線y1、 y2于點E、F,當E、F兩點間的距離不超過4時,求t的取值范圍.
軸,分別交直線y1、 y2于點E、F,當E、F兩點間的距離不超過4時,求t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B、F為圓心,大于![]() 長為半徑畫弧,兩弧交于一點P,連接AP并延長交BC于點E,連接EF.
長為半徑畫弧,兩弧交于一點P,連接AP并延長交BC于點E,連接EF.
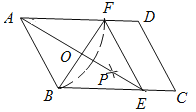
(1)四邊形ABEF是_______;(選填矩形、菱形、正方形、無法確定)(直接填寫結果)
(2)AE,BF相交于點O,若四邊形ABEF的周長為40,BF=10,則AE的長為________,∠ABC=________°.(直接填寫結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
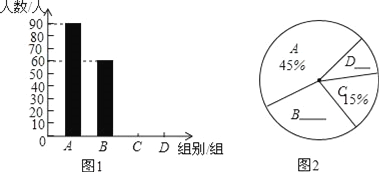
【題目】霧霾天氣嚴重影響市民的生活質量,在今年元旦期間,某校七年級一班的同學對“霧霾天氣的主要成因”就市民的看法做了隨機調查,并對調查結果進行了整理,繪制了不完整的統計圖表(如下圖),觀察分析并回答下列問題.
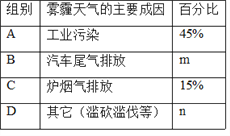
(1)本次被調查的市民共有 人;
(2)補全條形統計圖;
(3)圖2中區域B所對應的扇形圓心角為 度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,五邊形ABCDE中,AE∥BC,∠A+∠B=α,∠C+∠D+∠E=β,猜想α與β的數量關系并寫出你的證明.
(1)根據圖形寫出你的猜想: ;
(2)請證明你在(1)中寫出的猜想.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com