試題分析:延長DC,AB交于點F,作AG∥DE交DF于點G,四邊形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等邊三角形,四邊形AGDE是平行四邊形,求得等腰梯形AFDE的面積和△BCF的面積,二者的差就是所求五邊形的面積.
試題解析:延長DC,AB交于點F,作AG∥DE交DF于點G.

∵AE∥CD,∠A=∠E=120°,
∴四邊形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等邊三角形,四邊形AGDE是平行四邊形.設BF=x,
∵在直角△BCF中,∠BCF=90°-∠F=30°
∴FC=2x,
∴FD=2x+1.
∵平行四邊形AGDE中,DG=AE=2,
∴FG=2x-1,
∵△AFG是等邊三角形中,AF=FG,
∴x+1=2x-1,
解得:x=2.
在直角△BCF中,BC=BF•tanF=2

,
則S
△BCF=

BF•BC=

×2×2

=2

.
作AH⊥DF于點H.則AH=AF•sinF=3×

=
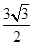
,
則S
梯形AFDE=

(AE+DF)•AH=

×(2+5)•
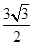
=

.
∴S
五邊形ABCDE=S
梯形AFDE-S
△BCF=

-

.
考點: 1.等腰梯形的性質;2.含30度角的直角三角形;3.勾股定理.


 .
.
 ,
, BF•BC=
BF•BC= ×2×2
×2×2 =2
=2 .
. =
=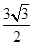 ,
, (AE+DF)•AH=
(AE+DF)•AH= ×(2+5)•
×(2+5)•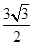 =
= .
. -
- .
.

