
【題目】問題情境
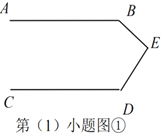
(1)如圖①,已知![]() ,試探究直線
,試探究直線![]() 與
與![]() 有怎樣的位置關系?并說明理由.
有怎樣的位置關系?并說明理由.
小明給出下面正確的解法:
直線![]() 與
與![]() 的位置關系是
的位置關系是![]() .
.
理由如下:
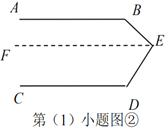
過點![]() 作
作![]() (如圖②所示)
(如圖②所示)
所以![]() (依據1)
(依據1)
因為![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依據2)
(依據2)
因為![]()
所以![]() (依據3)
(依據3)
交流反思
上述解答過程中的“依據1”,“依據2”,“依據3”分別指什么?
“依據1”:________________________________;
“依據2”:________________________________;
“依據3”:________________________________.
類比探究
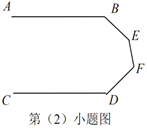
(2)如圖,當![]() 、
、![]() 、
、![]() 、
、![]() 滿足條件________時,有
滿足條件________時,有![]() .
.
拓展延伸
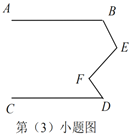
(3)如圖,當![]() 、
、![]() 、
、![]() 、
、![]() 滿足條件_________時,有
滿足條件_________時,有![]() .
.
【答案】(1)兩直線平行,同旁內角互補;同旁內角互補,兩直線平行;如果兩條直線都與第三條直線平行,那么這兩條直線也互相平行;(2)∠B+∠E+∠F+∠D=540°;(3)∠B+∠E+∠D-∠F=180°.
【解析】
(1)根據平行線的性質和判定,平行公理的推論回答即可;
(2)過點E、F分別作GE∥HF∥CD,根據兩直線平行,同旁內角互補及已知條件求得同旁內角∠ABE+∠BEG=180°,得到AB∥GE,再根據平行線的傳遞性來證得AB∥CD;
(3)過點E、F分別作ME∥FN∥CD,根據兩直線平行,內錯角相等及已知條件求得同旁內角∠B+∠BEM=180°,得到AB∥ME,再根據平行線的傳遞性來證得AB∥CD.
解:(1)由題意可知:“依據1”:兩直線平行,同旁內角互補;
“依據2”: 同旁內角互補,兩直線平行;
“依據3”: 如果兩條直線都與第三條直線平行,那么這兩條直線也互相平行;
(2)當∠B、∠E、∠F、∠D滿足條件∠B+∠E+∠F+∠D=540°時,有AB∥CD.
理由:如圖,過點E、F分別作GE∥HF∥CD,
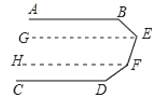
則∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠BEF+∠EFD+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
(3)當∠B、∠E、∠F、∠D滿足條件∠B+∠E+∠D-∠F=180°時,有AB∥CD.
如圖,過點E、F分別作ME∥FN∥CD,
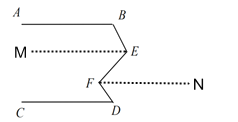
則∠MEF=EFN,∠D=∠DFN,
∵∠B+∠BEF+∠D-∠EFD=180°,
∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,
∴∠B+∠BEM=180°,
∴AB∥ME,
∴AB∥CD.


 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:初中數學 來源: 題型:
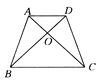
【題目】如圖所示,在四邊形ABCD中,已知AB與 CD不平行,∠ABD=∠ACD,請你添加一個條件:______ ,使的加上這個條件后能夠推出AD∥BC ,且AB=CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,B、D為線段AH上兩點,△ABC、△BDE和△DGH都是等邊三角形,連結CE并延長交AH的延長線于點F,點G恰好在CF上,△ABC的外接圓⊙O交CF于點M.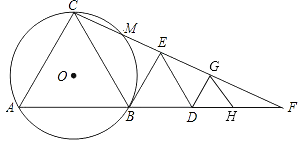
(1)求證:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圓O的半徑長;
,求圓O的半徑長;
(3)設等邊△ABC、△BDE、△DGH的面積分別為S1、S2、S3 , 請直接寫出S1、S2、S3之間的等量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD平分∠BAC,
(1)圖①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度數.
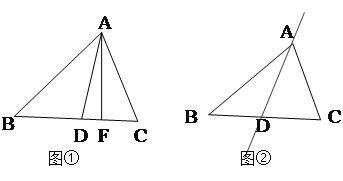
(2)圖②中,請你在直線AD上任意取一點E(不與點A、D重合),畫EF⊥BC,垂足為F.已知∠B=α,∠C=β(β>a).求∠DEF的度數. (用α、β的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列四幅圖象近似刻畫兩個變量之間的關系,請按圖象順序將下面四種情景與之對應排序( ).
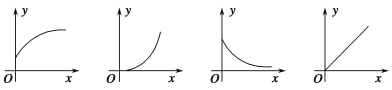
①一輛汽車在公路上勻速行駛(汽車行駛的路程與時間的關系)
②向錐形瓶中勻速注水(水面的高度與注水時間的關系)
③將常溫下的溫度計插入一杯熱水中(溫度計的讀數與時間的關系)
④一杯越來越涼的水(水溫與時間的關系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我省教育廳下發了![]() 在全省中小學幼兒園廣泛開展節約教育的通知
在全省中小學幼兒園廣泛開展節約教育的通知![]() ,通知中要求各學校全面持續開展“光盤行動”
,通知中要求各學校全面持續開展“光盤行動”![]() 深圳市教育局督導組為了調查學生對“節約教育”內容的了解程度
深圳市教育局督導組為了調查學生對“節約教育”內容的了解程度![]() 程度分為:“A:了解很多”、“B:了解較多”、“C:了解較少”、“D:不了解”
程度分為:“A:了解很多”、“B:了解較多”、“C:了解較少”、“D:不了解”![]() ,對本市某所中學的學生進行了抽樣調查
,對本市某所中學的學生進行了抽樣調查![]() 我們將這次調查的結果繪制了以下兩幅不完整統計圖:
我們將這次調查的結果繪制了以下兩幅不完整統計圖:
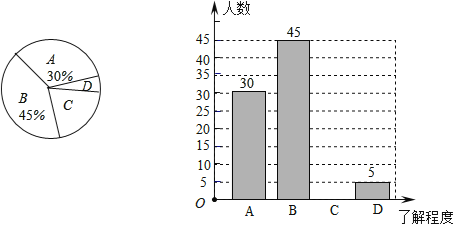
根據以上信息,解答下列問題:
![]() 補全條形統計圖;
補全條形統計圖;
![]() 本次抽樣調查了______名學生;在扇形統計圖中,求出“D”的部分所對應的圓心角度數.
本次抽樣調查了______名學生;在扇形統計圖中,求出“D”的部分所對應的圓心角度數.
![]() 若該中學共有2000名學生,請你估計這所中學的所有學生中,對“節約教育”內容“了解較少”的有多少人.
若該中學共有2000名學生,請你估計這所中學的所有學生中,對“節約教育”內容“了解較少”的有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個有45°角的三角板的直角頂點放在一張寬為3cm的紙帶邊沿上,另一個頂
點在紙帶的另一邊沿上,測得三角板的一邊與紙帶的一邊所在的直線成30°角,如圖(3),
則三角板的最大邊的長為( )

A. ![]() B.
B. ![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AC,BD為對角線,AB=BC=AC=BD,則∠ADC的大小為( )
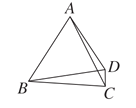
A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com