
【題目】某學校要在圍墻旁建一個長方形的中藥材種植實習苗圃,苗圃的一邊靠圍墻(墻的長度不限),另三邊用木欄圍成,建成的苗圃為如圖所示的長方形ABCD.已知木欄總長為120米,設AB邊的長為x米,長方形ABCD的面積為S平方米. 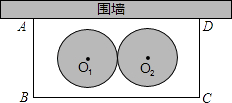
(1)求S與x之間的函數關系式(不要求寫出自變量x的取值范圍).當x為何值時,S取得最值(請指出是最大值還是最小值)?并求出這個最值;
(2)學校計劃將苗圃內藥材種植區域設計為如圖所示的兩個相外切的等圓,其圓心分別為O1和O2 , 且O1到AB、BC、AD的距離與O2到CD、BC、AD的距離都相等,并要求在苗圃內藥材種植區域外四周至少要留夠0.5米寬的平直路面,以方便同學們參觀學習.當(l)中S取得最值時,請問這個設計是否可行?若可行,求出圓的半徑;若不可行,請說明理由.
【答案】
(1)解:∵AB=x,∴BC=120﹣2x,
∴S=x(120﹣2x)=﹣2x2+120x;
當x= ![]() =30時,S有最大值為
=30時,S有最大值為 ![]() =1800
=1800
(2)解:設圓的半徑為r米,路面寬為a米,
根據題意得: ![]()
解得: ![]()
∵路面寬至少要留夠0.5米寬,
∴這個設計不可行
【解析】(1)表示出BC的長120﹣2x,由矩形的面積公式得出答案;(2)設出圓的半徑和藥材種植區外四中平面路面的寬,利用題目中的等量關系列出二元一次方程組,求得半徑和路面寬,當路面寬滿足題目要求時,方案可行,否則不行.
【考點精析】通過靈活運用相切兩圓的性質,掌握如果兩圓相切,那么切點一定在連心線上,它們是軸對稱圖形,對稱軸是兩圓的連心線即可以解答此題.


科目:初中數學 來源: 題型:
【題目】已知:如圖E在△ABC的邊AC上,且∠AEB=∠ABC.
⑴求證:∠ABE=∠C;
⑵若∠BAE的平分線AF交BE于F,FD∥BC交AC于D,設AB=5,AC=8,求DC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,其中真命題的個數是( )
①平面直角坐標系內的點與實數對一一對應;
②內錯角相等;
③平行于同一條直線的兩條直線互相平行;
④對頂角相等
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列敘述正確的是( )
A. 符號不同的兩個數是互為相反數
B. 一個有理數的相反數一定是負有理數
C. 2![]() 與2.75都是﹣
與2.75都是﹣![]() 的相反數
的相反數
D. 0沒有相反數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1在平面直角坐標系中,直線l1與y軸交于點A,點B(﹣3,3)也在直線l1上,將點B先向右平移1個單位長度,再向下平移2個單位長度得到點C,點C恰好也在直線l1上.

(1)求點C的坐標和直線l1的解析式;
(2)若將點C先向左平移3個單位長度,再向上平移6個單位長度得到點D,請你判斷點D是否在直線l1上;
(3)已知直線l2:y=x+b經過點B,與y軸交于點E,求△ABE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com