
已知:在△ABC中,∠CAB=![]() ,且
,且![]() ,AP平分∠CAB.
,AP平分∠CAB.
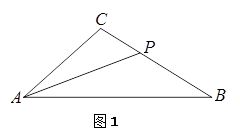
1.如圖1,若![]() ,∠ABC=32°,且AP交BC于點P,試探究線段
,∠ABC=32°,且AP交BC于點P,試探究線段
AB,AC與PB之間的數量關系,并對你的結論加以證明;
答:線段AB,AC與PB之間的數量關系為:___________________________.
2.如圖2,若∠ABC=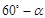 ,點P在△ABC的內部,且使∠CBP=30°,
,點P在△ABC的內部,且使∠CBP=30°,
求∠APC的度數(用含![]() 的代數式表示)
的代數式表示)

1.AB-AC= AB-AD=DB=PB
2.∠APC=120°+![]() ∠APC=120°+
∠APC=120°+![]()
解析:解:(1)AB-AC= PB;
證明:在AB上截取AD,使AD=AC.(如圖7)
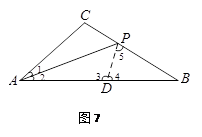 ∵AP平分∠CAB,
∵AP平分∠CAB,
∴∠1=∠2.
在△ACP和△ADP中,
![]() AC =AD,
AC =AD,
∠1 =∠2,
AP=AP,
∴△ACP≌△ADP.
∴∠C =∠3.
∵△ABC中,∠CAB=![]() =2×21°=42°,∠ABC=32°,
=2×21°=42°,∠ABC=32°,
∴∠C =180°-∠CAB-∠ABC=180°-42°-32° = 106°.
∴∠3 =106°.
∴∠4 =180°-∠3=180°-106°=74°,
∠5 =∠3-∠ABC=106°-32°=74°.
∴∠4 =∠5.
∴PB=DB.
∴AB-AC= AB-AD=DB=PB.
(2)方法一:延長AC至M,使AM=AB,連接PM,BM.(如圖8)
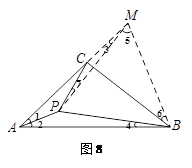
∵AP平分∠CAB,∠CAB=![]() ,
,
∴∠1=∠2=![]() =
=![]() .
.
在△AMP和△ABP中,
![]() AM =AB,
AM =AB,
∠1 =∠2,
AP=AP,
∴△AMP≌△ABP.
∴PM=PB,∠3 =∠4.
∵∠ABC=60°-![]() ,∠CBP=30°,
,∠CBP=30°,
∴∠4=(60°-![]() )-30° =30°-
)-30° =30°-![]() .
.
∴∠3 =∠4 =30°-![]() . ∵△AMB中,AM=AB,
. ∵△AMB中,AM=AB,
∴∠AMB=∠ABM =(180°-∠MAB)÷2=(180°-![]() )÷2 =90°-
)÷2 =90°-![]() .
.
∴∠5=∠AMB-∠3= (90°-![]() )-(30°-
)-(30°-![]() )=60°.
)=60°.
∴△PMB為等邊三角形.
∵∠6=∠ABM-∠ABC = (90°-![]() )-(60°-
)-(60°-![]() )=30°,
)=30°,
∴∠6=∠CBP.
∴BC平分∠PBM.
∴BC垂直平分PM.
∴CP=CM.
∴∠7 =∠3 = 30°-![]() .
.
∴∠ACP=∠7+∠3=(30°-![]() )+(30°-
)+(30°-![]() )=60°-
)=60°-![]() .
.
∴△ACP中,∠APC=180°-∠1-∠ACP
=180°-![]() -(60°-
-(60°-![]() )
)
=120°+![]() .
.
方法二:在AB上截取AM,使AM=AC,連接PM,延長AP交BC于N,連接MN.(如圖9)
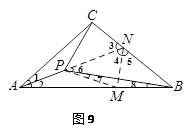
∵AP平分∠CAB,∠CAB=![]() ,
,
∴∠1=∠2=![]() =
=![]() .
.
在△ACN和△AMN中,
![]() AC =AM,
AC =AM,
∠1 =∠2,
AN=AN,
∴△ACN≌△AMN.
∴∠3 =∠4.
∵∠ABC=60°-![]() ,
,
∴∠3=∠2+∠NBA=![]() +(60°-
+(60°-![]() ) =60°.
) =60°.
∴∠3 =∠4 =60°.
∴∠5=180°-∠3-∠4=180°-60°-60°=60°.
∴∠4 =∠5. -∴NM平分∠PNB.
∵∠CBP=30°,
∴∠6=∠3-∠NBP=60°-30°=30°.
∴∠6=∠NBP.
∴NP=NB.
∴NM垂直平分PB.
∴MP=MB.
∴∠7 =∠8.
∴∠6+∠7 =∠NBP+∠8,
即∠NPM=∠NBM=60°-![]() . ∴∠APM=180°-∠NPM =180°-(60°-
. ∴∠APM=180°-∠NPM =180°-(60°-![]() )=120°+
)=120°+![]() .
.
在△ACP和△AMP中,
![]() AC =AM,
AC =AM,
∠1 =∠2,
AP=AP,
∴△ACP≌△AMP.
∴∠APC=∠APM .
∴∠APC=120°+![]() .
.


科目:初中數學 來源: 題型:
 (1)化簡:(a-
(1)化簡:(a-| 1 |
| a |
| a2-2a+1 |
| a |
查看答案和解析>>
科目:初中數學 來源: 題型:
 20、如圖,已知,在△ABC中,∠ABC和∠ACB的平分線交于點M,ME∥AB交BC于點E,MF∥AC交BC于點F.求證:△MEF的周長等于BC的長.
20、如圖,已知,在△ABC中,∠ABC和∠ACB的平分線交于點M,ME∥AB交BC于點E,MF∥AC交BC于點F.求證:△MEF的周長等于BC的長.查看答案和解析>>
科目:初中數學 來源: 題型:
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足為點E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足為點E.∠B=38°,∠C=70°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com