
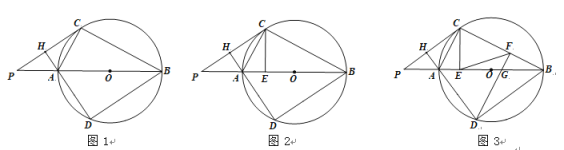
【題目】在⊙O 中,AB 為直徑,點 P 在BA 的延長線上,PC 為⊙O 的切線,過點 A 作AH⊥PC 于點 H, 交⊙O 于點 D,連接 BC、BD、AC.
(1)如圖 1,求證:∠CAH=∠CAB;
(2)如圖 2,過點 C 作 CE⊥AB 于點 E,求證:BD=2CE;
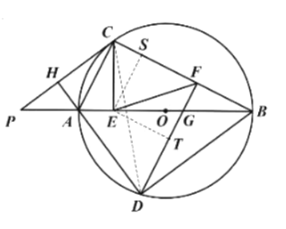
(3)如圖 3,在(2)的條件下,點 F 在BC 上,連接 DF、EF,若 BG=2AE,∠CFE=45°,OG=1,求線段 EF 的長.
【答案】(1)見解析;(2)見解析;(3)![]() .
.
【解析】
(1)連接OC,根據切線的性質證得![]() ,利用半徑相等即可證明;
,利用半徑相等即可證明;
(2)延長CO交BD于點M,根據角平分線的性質證得![]() ,證得四邊形
,證得四邊形![]() 為矩形,推出
為矩形,推出![]() ,
,![]() ,
,![]() ,利用垂徑定理即可證明;
,利用垂徑定理即可證明;
(3)連接CD,過點E作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,設
,設![]() ,則
,則![]() ,
,![]() ,由
,由![]() ,推出
,推出![]() ,
,![]() ,即
,即![]() ,再推出
,再推出![]() ,證得
,證得![]() ,得到
,得到![]() ,在
,在![]() 中,利用勾股定理求得
中,利用勾股定理求得![]() ,然后解直角三角形即可求解.
,然后解直角三角形即可求解.
(1)證明:連接OC,
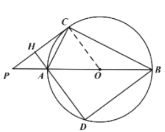
∵PC為圓O的切線,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)證明:連接OC,延長CO交BD于點M,
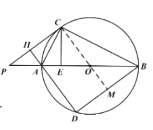
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵AB為直徑,
∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 為矩形,
為矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
(3)解:連接CD,過點E作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴設![]() ,則
,則![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB為圓O的直徑,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△BSE中,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
在Rt△FSE中,![]() ,
,![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
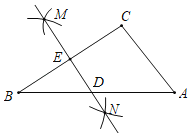
【題目】如圖,在△ABC中,按以下步驟作圖:①分別以點B和點C為圓心,大于![]() BC的長為半徑作弧,兩弧相交于點M和N;②作直線MN,分別交邊AB,BC于點D和E,連接CD.若∠BCA=90°,AB=8,則CD的長為_____.
BC的長為半徑作弧,兩弧相交于點M和N;②作直線MN,分別交邊AB,BC于點D和E,連接CD.若∠BCA=90°,AB=8,則CD的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了弘揚中國傳統文化,某校對全校學生進行了古詩詞知識測試,將測試成績分為一般、良好、優秀三個等級.從中隨機抽取部分學生的測試成績,繪制成如下兩幅統計圖,根據圖中的信息,解答下列問題:
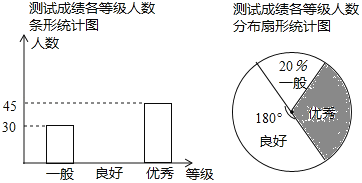
(1)本次抽樣調查的樣本容量是 ,扇形統計圖中陰影部分扇形的圓心角是 度;
(2)將條形統計圖補充完整;
(3)根據本次抽樣調查的結果,試估計該校2000名學生中測試成績為良好和優秀的共有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
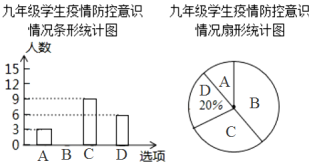
【題目】九年級復學復課后,某校為了了解學生的疫情防控意識情況,在全校九年級隨機抽取部分學生進行問卷調查.根據調查結果,把學生的防控意識分成“A.很強”、“B.較強”、“C.一般”、“D.淡薄”四個層次,將調查的結果繪制如下兩幅不完整的統計圖,請根據圖中的信息,解答下列問題:
(1)本次共調查了 名學生,并將條形統計圖補充完整;
(2)如果把疫情防控意識“很強或較強”視為合格,該校九年級共有600名學生,請你估計合格的學生約有多少名?
(3)在“A.很強”的3人中,有2名女生,1名男生,老師想從這3人中任選兩人做宣傳員,請用列表或畫樹狀圖法求出被選中的兩人恰好是一男生一女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
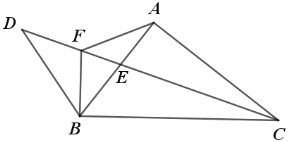
【題目】如圖,Rt△ABC 中,∠BAC=90°,CE 平分∠ACB,點 D 在 CE的延長線上,連接 BD,過B作BF⊥BC交 CD 于點 F,連接 AF,若CF=2BD ,DE:CE=5:8 , BF ![]() ,則AF的長為_________.
,則AF的長為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
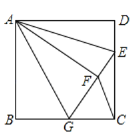
【題目】如圖,已知正方形ABCD的邊長為a,E為CD邊上一點(不與端點重合),將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,CF.給出下列判斷:①∠EAG=45°;②若DE=![]() a,則AG∥CF;③若E為CD的中點,則△GFC的面積為
a,則AG∥CF;③若E為CD的中點,則△GFC的面積為![]() a2;④若CF=FG,則
a2;④若CF=FG,則![]() ;⑤BGDE+AFGE=a2.其中正確的是____________.(寫出所有正確判斷的序號)
;⑤BGDE+AFGE=a2.其中正確的是____________.(寫出所有正確判斷的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情期間,“線上教學”為我們提供了復習的渠道.學校隨機抽取部分學生就“你是否喜歡線上教學”進行了問卷調查,并將調查結果統計后繪制成如下統計表和統計圖.
調查結果統計表
類別 | 非常喜歡 | 喜歡 | 一般 | 不喜歡 |
頻數 | a | 70 | 20 | 10 |
頻率 | 0.5 | b | 0.15 | |
調查結果扇形統計圖

(1)在統計表中,a= ;b= ;
(2)在扇形統計圖中,對線上教學感覺“一般”所對應的圓心角度數為 ;
(3)已知全校共有3000名學生,試估計“喜歡”線上教學的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為落實“垃圾分類”,環衛部門要求垃圾要按A,B,C三類分別裝袋,投放,其中A類指廢電池,過期藥品等有毒垃圾,B類指剩余食品等廚余垃圾,C類指塑料,廢紙等可回收垃圾.甲投放了一袋垃圾,乙投放了兩袋垃圾,這兩袋垃圾不同類.
(1)直接寫出甲投放的垃圾恰好是A類的概率;
(2)求乙投放的垃圾恰有一袋與甲投放的垃圾是同類的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com