
【題目】已知:a、b、c是△ABC的三邊長,化簡 ![]() .
.
【答案】解:∵a、b、c是△ABC的三邊長, ∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|﹣|b+c﹣a|+|c﹣b﹣a|
=a+b+c﹣(b+c﹣a)+(b+a﹣c)
=a+b+c﹣b﹣c+a+b+a﹣c
=3a+b﹣c.
【解析】根據三角形的三邊關系定理得出a+b>c,b+c>a,b+a>c,根據二次根式的性質得出含有絕對值的式子,最后去絕對值符號后合并即可.
【考點精析】本題主要考查了二次根式的性質與化簡和三角形三邊關系的相關知識點,需要掌握1、如果被開方數是分數(包括小數)或分式,先利用商的算數平方根的性質把它寫成分式的形式,然后利用分母有理化進行化簡.2、如果被開方數是整數或整式,先將他們分解因數或因式,然后把能開得盡方的因數或因式開出來;三角形兩邊之和大于第三邊;三角形兩邊之差小于第三邊;不符合定理的三條線段,不能組成三角形的三邊才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,將△ABC繞點A順時針旋轉90°后得到的△AB′C′(點B的對應點是點B′,點C的對應點是點C′),連接CC′.若∠CC′B′=32°,則∠B的大小是( )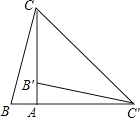
A.32°
B.64°
C.77°
D.87°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC, ①如圖1,若P點是∠ABC和∠ACB的角平分線的交點,則∠P=90°+ ![]() ∠A;
∠A;
②如圖2,若P點是∠ABC和外角∠ACE的角平分線的交點,則∠P=90°﹣∠A;
③如圖3,若P點是外角∠CBF和∠BCE的角平分線的交點,則∠P=90°﹣ ![]() ∠A.
∠A.
上述說法正確的個數是( )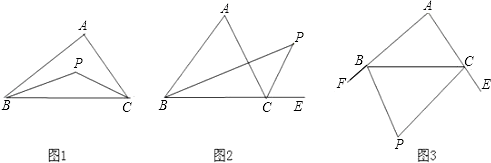
A.3個
B.2個
C.1個
D.0個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,我們把點P(x,y)的橫坐標與縱坐標的絕對值之和叫做點P(x,y)的勾股值,記為:「P」,即「P」=|x|+|y|.
(1)求點A(﹣1,3)的勾股值「A」;
(2)若點B在第一象限且滿足「B」=3,求滿足條件的所有B點與坐標軸圍成的圖形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com