【題目】如圖所示，在平面直角坐標系中A（0，0），B（2，0），△AP1B是等腰直角三角形，且∠P1=90°，把△AP1B繞點B順時針旋轉180°，得到△BP2C；把△BP2C繞點C順時針旋轉180°，得到△CP3D，依此類推，則旋轉第2017次后，得到的等腰直角三角形的直角頂點P2018的坐標為（ ）
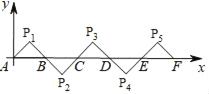
A. （4030，1） B. （4029，﹣1）
C. （4033，1） D. （4035，﹣1）
科目：初中數學 來源： 題型：
【題目】（2017重慶A卷第11題）如圖，小王在長江邊某瞭望臺D處，測得江面上的漁船A的俯角為40°，若DE=3米，CE=2米，CE平行于江面AB，迎水坡BC的坡度i=1：0.75，坡長BC=10米，則此時AB的長約為（ ）（參考數據：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）．
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，△ABC的三個頂點的坐標分別為A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．
（1）在平面直角坐標系中畫出與△ABC關于點P（1，0）成中心對稱的△A'B'C'，并分別寫出點A'，B'，C'的坐標；
（2）如果點M（a，b）是△ABC邊上（不與A，B，C重合）任意一點，請寫出在△A'B'C'上與點M對應的點M'的坐標．
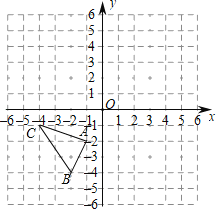
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y=ax2+2x+c圖象經過點A （1，4）和點C （0，3）．
（1）求該二次函數的解析式；
（2）結合函數圖象，直接回答下列問題：
①當﹣1＜x＜2時，求函數y的取值范圍： ．
②當y≥3時，求x的取值范圍： ．
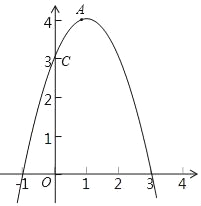
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=﹣x2+bx+c與一直線相交于A（﹣1，0）、C（2，3）兩點，與y軸交于點N，其頂點為D．
（1）求拋物線及直線AC的函數關系式；
（2）若P是拋物線上位于直線AC上方的一個動點，求△APC的面積的最大值及此時點P的坐標；
（3）設點M（3，n），求使MN+MD取最小值時n的值．
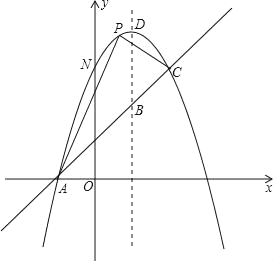
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于代數式，不同的表達形式能表現出它的不同性質．例如代數式
，若將其寫成
的形式，就能看出不論字母x取何值，它都表示正數；若將它寫成
的形式，就能與代數式B=
建立聯系．下面我們改變x的值，研究一下A，B兩個代數式取值的規律：
x | -2 | -1 | 0 | 1 | 2 | 3 |
| 10 | 5 | 2 | 1 | 5 | |
| 17 | 10 | 5 |
（1）完成上表；
（2）觀察表格可以發現：
若x=m時，
，則x=m+1時，
．我們把這種現象稱為代數式A參照代數式B取值延后，此時延后值為1．
①若代數式D參照代數式B取值延后，相應的延后值為2，求代數式D；
②已知代數式
參照代數式
取值延后，請直接寫出b-c的值：________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩人加工同一種零件，甲每天加工的數量是乙每天加工數量的 1.5 倍，兩人各加工 600 個這種零件，甲比乙少用 5 天．
（1）求甲、乙兩人每天各加工多少個這種零件？
（2）已知甲、乙兩人加工這種零件每天的加工費分別是 150 元和 120 元，現有 3000 個這種零件的加工任務，甲單獨加工一段時間后另有安排，剩余任務由乙單獨完成．如果總加工費不超過 7800 元，那么甲至少加工了多少天？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
