
【題目】如果方程x2+px+q=0的兩個根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,請根據以上結論,解決下列問題:
(1)已知關于x的方程x2+mx+n=0,(n≠0),求出一個一元二次方程,使它的兩個根分別是已知方程兩根的倒數;
(2)已知a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() 的值;
的值;
(3)已知a、b、c滿足a+b+c=0,abc=16,求正數c的最小值.
【答案】
(1)解:設方程x2+mx+n=0,(n≠0)的兩個根分別是x1,x2,
則: ![]() +
+ ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
![]()
![]() =
= ![]() =
= ![]() ,
,
若一個一元二次方程的兩個根分別是已知方程兩根的倒數,
則這個一元二次方程是:x2+ ![]() x+
x+ ![]() =0
=0
(2)解:∵a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,
∴a,b是x2﹣15x﹣5=0的解,
當a≠b時,a+b=15,ab=﹣5,
![]() =
= ![]() =
= ![]() =
= ![]() =﹣47.
=﹣47.
當a=b時,原式=2
(3)解:∵a+b+c=0,abc=16,
∴a+b=﹣c,ab= ![]() ,
,
∴a、b是方程x2+cx+ ![]() =0的解,
=0的解,
∴c2﹣4 ![]() ≥0,
≥0,
c2﹣ ![]() ≥0,
≥0,
∵c是正數,
∴c3﹣43≥0,
c3≥43,
c≥4,
∴正數c的最小值是4
【解析】(1)先設方程x2+mx+n=0,(n≠0)的兩個根分別是x1 , x2 , 得出 ![]() +
+ ![]() =﹣
=﹣ ![]() ,
, ![]()
![]() =
= ![]() ,再根據這個一元二次方程的兩個根分別是已知方程兩根的倒數,即可求出答案.(2)根據a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,得出a,b是x2﹣15x﹣5=0的解,求出a+b和ab的值,即可求出
,再根據這個一元二次方程的兩個根分別是已知方程兩根的倒數,即可求出答案.(2)根據a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,得出a,b是x2﹣15x﹣5=0的解,求出a+b和ab的值,即可求出 ![]() 的值.(3)根據a+b+c=0,abc=16,得出a+b=﹣c,ab=
的值.(3)根據a+b+c=0,abc=16,得出a+b=﹣c,ab= ![]() ,a、b是方程x2+cx+
,a、b是方程x2+cx+ ![]() =0的解,再根據c2﹣4
=0的解,再根據c2﹣4 ![]() ≥0,即可求出c的最小值.
≥0,即可求出c的最小值.
【考點精析】解答此題的關鍵在于理解求根公式的相關知識,掌握根的判別式△=b2-4ac,這里可以分為3種情況:1、當△>0時,一元二次方程有2個不相等的實數根2、當△=0時,一元二次方程有2個相同的實數根3、當△<0時,一元二次方程沒有實數根,以及對根與系數的關系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商.


科目:初中數學 來源: 題型:
【題目】如圖,將△ABC沿DE、EF翻折,頂點A,B均落在點O處,且EA與EB重合于線段EO,若∠CDO+∠CFO=78°,則∠C的度數為=___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為64,E、F、G分別為AB、AC、BC的中點,A′、B′、C′分別為EF、EG、GF的中點,△A′B′C′的周長為_________.如果△ABC、△EFG、△A′B′C′分別為第1個、第2個、第3個三角形,按照上述方法繼續作三角形,那么第n個三角形的周長是__________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
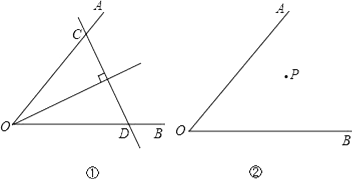
【題目】已知∠AOB及其內部一點P,試討論以下問題的解答:
(1)如圖①,若點P在∠AOB的平分線上,我們可以過P點作直線垂直于角平分線,分別交OA、OB于點C、D,則可以得到△OCD是以CD為底邊的等腰三角形;若點P不在∠AOB的平分線上(如圖②),你能過P點作直線,分別交OA、OB于點C、D,得到△OCD是等腰三角形,且CD是底邊嗎?請你在圖②中畫出圖形,并簡要說明畫法.
(2)若點P不在∠AOB的平分線上(如圖③),我們可以過P點作PQ∥OA,并作∠QPR=∠AOB,直線PR分別交OA、OB于點C、D,則可以得到△OCD是以OC為底的等腰三角形.請你說明這樣作的理由.
(3)若點P不在∠AOB的平分線上,請你利用在(2)中學到的方法,在圖④中過P點作直線分別交OA、OB于點C、D,使得△OCD是等腰三角形,且OD是底邊.保留畫圖的痕跡,不用寫出畫法.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一根40cm的金屬棒,欲將其截成x根7cm的小段和y根9cm的小段,剩余部分作廢料處理,若使廢料最少,則正整數x,y應分別為 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,D是BC延長線上一點,E是BD垂直平分線與AB的交點,DE交AC于點F.求證:點E在AF的垂直平分線上.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com