
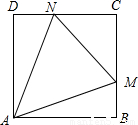
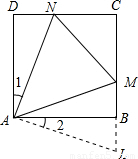
 解:(1)如圖,延長CB至L,使BL=DN,則Rt△ABL≌Rt△AND,故AL=AN,
解:(1)如圖,延長CB至L,使BL=DN,則Rt△ABL≌Rt△AND,故AL=AN,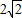 )(z+2-
)(z+2-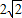 )≥0
)≥0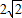 -2當且僅當x=y=2-
-2當且僅當x=y=2-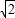 時等號成立
時等號成立 ML•AB=
ML•AB= z
z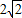 -2,x=y=2-
-2,x=y=2-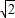 時,S△AMN取到最小值為
時,S△AMN取到最小值為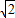 -1.
-1.

 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:初中數學 來源: 題型:
 4、如圖所示,正方形ABCD中,E,F是對角線AC上兩點,連接BE,BF,DE,DF,則添加下列哪一個條件可以判定四邊形BEDF是菱形( )
4、如圖所示,正方形ABCD中,E,F是對角線AC上兩點,連接BE,BF,DE,DF,則添加下列哪一個條件可以判定四邊形BEDF是菱形( )查看答案和解析>>
科目:初中數學 來源: 題型:
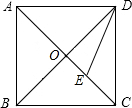 如圖所示,正方形ABCD的對角線AC,BD相交于點O,DE平分∠ODC交OC于點E,若AB=2,則線段OE的長為( )
如圖所示,正方形ABCD的對角線AC,BD相交于點O,DE平分∠ODC交OC于點E,若AB=2,則線段OE的長為( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,正方形ABCD的邊長為1,點E為AB的中點,以E為圓心,1為半徑作圓,分別交AD,BC于M,N兩點,與DC切于點P,則圖中陰影部分面積是
如圖所示,正方形ABCD的邊長為1,點E為AB的中點,以E為圓心,1為半徑作圓,分別交AD,BC于M,N兩點,與DC切于點P,則圖中陰影部分面積是查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示的正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:
如圖所示的正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com