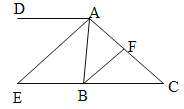
【題目】如圖，在Rt△ABC中，∠B＝90，AB＝6，BC＝8．以AB， BC，AC的中點A1，B1，C1構成△A1B1C1，以A1B，BB1，A1B1的中點A2，B2，C2構成△A2B2C2，……依次操作，陰影部分面積之和將接近 ( )
A. 7 B. 8 C. 9 D. 10
【答案】B
【解析】
由已知易得S△ABC=24，S△A1B1C1=S△A1B1B=
S△ABC=6，同理可得：S△A2B2C2=S△A2B2B=S△A1B1B=1.5，S△A3B3C3=
……，然后將所得的式子相加，化簡即可得到所求結果.
∵在Rt△ABC中，∠B＝90，AB＝6，BC＝8，
∴S△ABC=
，
∵△A1B1C1是以AB， BC，AC的中點A1，B1，C1構成的，
∴S△A1B1C1=S△A1B1B=S△ABC=6，
同理可得：S△A2B2C2=6×=1.5，S△A3B3C3=，S△A4B4C4=
，S△A5B5C5=
，……，
∴S陰影= S△A1B1C1+S△A2B2C2+S△A3B3C3+S△A4B4C4+S△A5B5C5+……=6+1.5+0.375+0.09375+0.0234375+……≈8.
故選B.
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】甲乙兩人同時登山，甲、乙兩人距地面的高度y（米）與登山時間x（分）之間的函數圖像如圖所示，根據圖像所提供的信息解答下列問題：
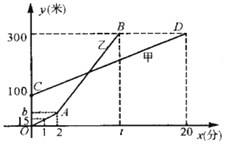
（1）甲登山的速度是每分鐘 米，乙在A地提速時距地面的高度b為 米．
（2）若乙提速后，乙的速度是甲登山速度的3倍，請分別求出甲、乙二人登山全過程中，登山時距地面的高度y（米）與登山時間x（分）之間的函數關系式．
（3）登山多長時間時，乙追上了甲？此時乙距A地的高度為多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
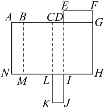
【題目】如圖所示是長方體的平面展開圖．
(1)將平面展開圖折疊成一個長方體，與字母N重合的點有哪幾個？
(2)若AG＝CK＝14 cm，FG＝2 cm，LK＝5 cm，則該長方體的表面積和體積分別是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有甲、乙、丙等多家食品公司在某市開設蛋糕店，該市蛋糕店數量的扇形統計圖如圖所示，其中統計圖中沒有標注相應公司數量的百分比．已知乙公司經營150家蛋糕店，請根據該統計圖回答下列問題：
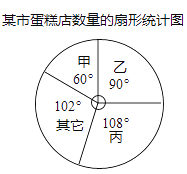
（1）求甲公司經營的蛋糕店數量和該市蛋糕店的總數；
（2）甲公司為了擴大市場占有率，決定在該市增設蛋糕店數量達到全市的20%，求甲公司需要增設的蛋糕店數量．
查看答案和解析>>
科目：初中數學 來源： 題型：
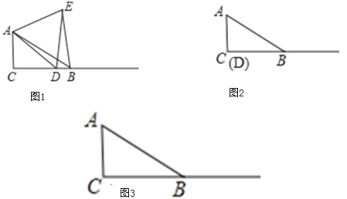
【題目】問題：如圖1，在Rt△ABC中，∠C=90°，∠ABC=30°，點D是邊CB上任意一點，△ADE是等邊三角形，且點E在∠ACB的內部，連接BE．探究線段BE與DE之間的數量關系．請你完成下列探究過程：先將圖形特殊化，得出猜想，再對一般情況進行分析并加以證明．
（1）當點D與點C重合時（如圖2），請你補全圖形．由∠BAC的度數為 ，點E落在 ______ ，容易得出BE與DE之間的數量關為 ；
（2）當點D是BC上任意一點（不與點B、C重合）時，結合圖1，探究（1）中線段BE與DE之間的數量關系是否還成立？并證明你的結論．
（3）如圖3，若點P為直線BC上一點，若△PAB為等腰三角形，請你求出∠APB的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列各式
（x﹣1）（x+1）＝x2﹣1
（x﹣1）（x2+x+1）＝x3﹣1
（x﹣1）（x3+x2+x+1）＝x4﹣1
（1）根據以上規律，則（x﹣1）（x6+x5+x4+x3+x2+x+1）＝ ；
（2）你能否由此歸納出一般規律（x﹣1）（xn+xn﹣1+……+x+1）＝ ；
（3）根據以上規律求32018+32017+32016+…32+3+1的結果．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
．
（1）若
，
平分
，求
的度數；
（2）若
平分，
平分
．
①求證
；
②將結論與條件互換位置，其他條件不變，組成一個新的命題，判斷該命題的真假，并寫出證明過程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
