
【題目】如圖,點A是⊙O直徑BD延長線上的一點,C在⊙O上,AC=BC,AD=CD
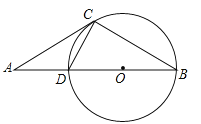
(1)求證:AC是⊙O的切線;
(2)若⊙O的半徑為4,求△ABC的面積.
【答案】(1)、證明過程見解析;(2)、12![]()
【解析】
試題分析:(1)、連接OC,根據AC=BC,AD=CD,OB=OC得出∠A=∠B=∠1=∠2,根據BD為直徑得出∠BCD=90°,從而說明∠ACO=90°,得出切線;(2)、首先根據題意得出△DCO是等邊三角形,根據Rt△BCD的勾股定理得出BC的長度,作CE⊥AB于點E,然后根據Rt△BEC的勾股定理得出CE的長度,然后求出△ABC的面積.
試題解析:(1)、如圖,連接OC. ∵AC=BC,AD=CD,OB=OC,∴∠A=∠B=∠1=∠2.
又∵BD是直徑, ∴∠BCD=90°,∵∠ACO=∠DCO+∠2, ∴∠ACO=∠DCO+∠1=∠BCD,
∴∠ACO=90°, 又C在⊙O上, ∴AC是⊙O的切線;
(2)、由題意可得△DCO是等腰三角形, ∵∠CDO=∠A+∠2,∠DOC=∠B+∠1,
∴∠CDO=∠DOC,即△DCO是等邊三角形. ∴∠A=∠B=∠1=∠2=30°,CD=AD=4,
在直角△BCD中,![]() . 作CE⊥AB于點E.在直角△BEC中,∠B=30°,
. 作CE⊥AB于點E.在直角△BEC中,∠B=30°,
∴CE=![]() BC=
BC=![]() , ∴S△ABC=
, ∴S△ABC=![]() ABCE=
ABCE=![]() ×12×2
×12×2![]() =12
=12![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,E、F分別為邊AB、CD的中點,BD是對角線.
(1)求證:△ADE≌△CBF;
(2)若∠ADB是直角,則四邊形BEDF是什么四邊形?證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC是邊長為4的正方形,點P從點O沿邊OA向點A運動,每秒運動1個單位.連結CP,過點P作PE⊥CP交AB于點D,且PE=PC,過點E作EF∥OA,交OB于點F,連結FD、BE,設點P運動的時間為![]()
![]() .
.
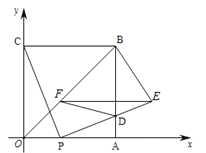
(1)點E的坐標為 (用含![]() 的代數式表示);
的代數式表示);
(2)試判斷線段EF的長度是否隨點P的運動變化而改變?并說明理由;
(3)當![]() 為何值時,四邊形BEDF的面積為
為何值時,四邊形BEDF的面積為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com