
【題目】如圖,直線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,與
,與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() .
.

(1)求點(diǎn)![]() ,
,![]() 的坐標(biāo);
的坐標(biāo);
(2)求當(dāng)![]() 時,
時,![]() 的值,當(dāng)
的值,當(dāng)![]() 時,
時,![]() 的值;
的值;
(3)過點(diǎn)![]() 作直線
作直線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,且使
,且使![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)![]() ,
,![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根據(jù)坐標(biāo)軸上點(diǎn)的坐標(biāo)特征確定![]() 點(diǎn)和
點(diǎn)和![]() 點(diǎn)坐標(biāo);
點(diǎn)坐標(biāo);
(2)把![]() 代入解析式即可求得
代入解析式即可求得![]() 的值;把
的值;把![]() 代入解析式,解得
代入解析式,解得![]() 的值即可;
的值即可;
(3)由![]() ,
,![]() 得到
得到![]() ,分類討論:當(dāng)點(diǎn)
,分類討論:當(dāng)點(diǎn)![]() 在
在![]() 軸正半軸上時,則
軸正半軸上時,則![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ;當(dāng)點(diǎn)
;當(dāng)點(diǎn)![]() 在
在![]() 軸負(fù)半軸上時,則
軸負(fù)半軸上時,則![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ,然后根據(jù)待定系數(shù)法求兩種情況下的直線解析式.
,然后根據(jù)待定系數(shù)法求兩種情況下的直線解析式.
解:(1)當(dāng)![]() 時,
時,![]() ,
,
得![]() ,則
,則![]() ,
,![]() .
.
當(dāng)![]() 時,
時,![]() ,則
,則![]() ;
;
(2)當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,則
時,則![]() ,解得
,解得![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,則點(diǎn)
,則點(diǎn)![]() 的位置有兩種情況,點(diǎn)
的位置有兩種情況,點(diǎn)![]() 在
在![]() 軸的正半軸上或點(diǎn)
軸的正半軸上或點(diǎn)![]() 在
在![]() 軸的負(fù)半軸上.
軸的負(fù)半軸上.
當(dāng)點(diǎn)![]() 在
在![]() 軸負(fù)半軸上時,
軸負(fù)半軸上時,![]() ,
,
則![]() 的面積為
的面積為![]() ;
;
當(dāng)點(diǎn)![]() 在
在![]() 軸的正半軸上時,
軸的正半軸上時,![]() ,
,
則![]() 的面積為
的面積為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場用3000元購進(jìn)某種商品,由于銷售狀況良好,商場又用9000元購進(jìn)這種商品,但這次的進(jìn)價比第一次的進(jìn)價提高了20%,購進(jìn)商品比第一次的2倍還多300千克,如果商場按每千克9元出售.
求:(1)該種商品第一次的進(jìn)價是每千克多少元?
(2)超市銷售完這種商品共盈利多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
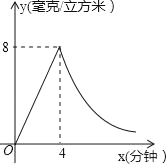
【題目】為了預(yù)防“流感”,某學(xué)校對教室采用藥熏法進(jìn)行消毒,已知藥物燃燒時,室內(nèi)每立方米空氣中的含藥量y(毫克/立方米)與藥物點(diǎn)燃后的時間x(分鐘)成正比例,藥物燃盡后,y與x成反比例(如圖所示).已知藥物點(diǎn)燃后4分鐘燃盡,此時室內(nèi)每立方米空氣中含藥量為8毫克.
(1)求藥物燃燒時,y與x之間函數(shù)的表達(dá)式;
(2)求藥物燃盡后,y與x之間函數(shù)的表達(dá)式;
(3)研究表明,當(dāng)空氣中每立方米的含藥量不低于2毫克時,才能有效殺滅空氣中的病菌,那么此次消毒有效時間有多長?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于點(diǎn)D,延長DB至點(diǎn)F,使BF=BD連接AF.
(1)求證:AF=CD.
(2)若CE平分∠ACB交AB于點(diǎn)E,試猜想AC,AF,AE三條線段之間的數(shù)量關(guān)系,并證明你的猜想.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知拋物線C1:![]() 與x軸的一個交點(diǎn)為A(-1,0),另一個交點(diǎn)為B,與
與x軸的一個交點(diǎn)為A(-1,0),另一個交點(diǎn)為B,與![]() 軸的交點(diǎn)為C(0,-3),其頂點(diǎn)為D.
軸的交點(diǎn)為C(0,-3),其頂點(diǎn)為D.
(1)求拋物線C1的解析式;
(2)如圖1,將△OBC沿![]() 軸向右平移m個單位長度(0﹤
軸向右平移m個單位長度(0﹤![]() ≤
≤![]() )得到另一個三角形△EFG,將△EFG與△BCD重疊部分(四邊形BPGQ)的面積記為S,用含m的代數(shù)式表示S;
)得到另一個三角形△EFG,將△EFG與△BCD重疊部分(四邊形BPGQ)的面積記為S,用含m的代數(shù)式表示S;
(3)如圖2,將拋物線C1平移,使其頂點(diǎn)為原點(diǎn)O,得到拋物線C2.若直線![]() 與拋物線C2交于S、T兩點(diǎn),點(diǎn)
與拋物線C2交于S、T兩點(diǎn),點(diǎn)![]() 是線段ST上一動點(diǎn)(不與S、T重合),試探究拋物線C2上是否存在一點(diǎn)R,點(diǎn)R關(guān)于點(diǎn)N的中心對稱點(diǎn)K也在拋物線C2上.
是線段ST上一動點(diǎn)(不與S、T重合),試探究拋物線C2上是否存在一點(diǎn)R,點(diǎn)R關(guān)于點(diǎn)N的中心對稱點(diǎn)K也在拋物線C2上.


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
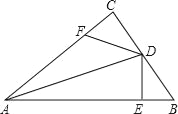
【題目】如圖,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于點(diǎn)E,點(diǎn)F在AC上,且BD=DF.
(1)求證:CF=EB;
(2)請你判斷AE、AF與BE之間的數(shù)量關(guān)系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,BD為△ABC的角平分線,且BD=BC,E為BD延長線上的一點(diǎn),BE=BA,過E作EF⊥AB,F(xiàn)為垂足,下列結(jié)論:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正確的結(jié)論有________(填序號).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面給出四個結(jié)論:①BE=CF;②AB=DC;③
,下面給出四個結(jié)論:①BE=CF;②AB=DC;③![]() ;
;
④四邊形ABCD是矩形.其中說法正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知y是x的反比例函數(shù),且點(diǎn)A(3,5)在這個函數(shù)的圖象上.
(1)求y與x之間的函數(shù)關(guān)系式;
(2)當(dāng)點(diǎn)B(-5,m)也在這個反比例函數(shù)的圖象上時,求△AOB的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com