
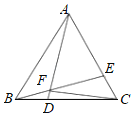
【題目】如圖,在等邊△ABC中,BD=CE,連接AD、BE交于點F.
(1)求∠AFE的度數;
(2)求證:ACDF=BDBF;
(3)連接FC,若CF⊥AD時,求證:BD=![]() DC.
DC.
【答案】(1)60°;(2)證明見解析;(3)證明見解析
【解析】
(1)證明△ABD≌△BCE(SAS),得出∠BAD=∠CBE,則∠BFD=∠AFE=∠ABC=60°;
(2)證明△ADB∽△BDF,得出![]() ,由AB=AC可得出結論;
,由AB=AC可得出結論;
(3)延長BE至H,使FH=AF,連接AH,CH,證明△BAF≌△CAH(SAS),得出∠ABF=∠ACH,CH=BF,可證明AF∥CH,得出![]() ,進而即可得出答案.
,進而即可得出答案.
解:(1)∵△ABC是等邊三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
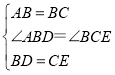 ,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠ABC,
∴∠BFD=∠AFE=∠ABC=60°;
(2)證明:由(1)知∠BAD=∠DBF,
又∵∠ADB=∠BDF,
∴△ADB∽△BDF,
∴![]() ,
,
又AB=AC,
∴![]() ,
,
∴ACDF=BDBF;
(3)證明:延長BE至H,使FH=AF,連接AH,CH,
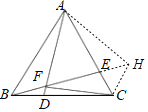
由(1)知∠AFE=60°,∠BAD=∠CBE,
∴△AFH是等邊三角形,
∴∠FAH=60°,AF=AH,
∴∠BAC=∠FAH=60°,
∴∠BAC﹣∠CAD=∠FAH﹣∠CAD,
即∠BAF=∠CAH,
在△BAF和△CAH中,
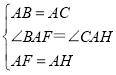 ,
,
∴△BAF≌△CAH(SAS),
∴∠ABF=∠ACH,CH=BF,
又∵∠ABC=∠BAC,∠BAD=∠CBE,
∴∠ABC﹣∠CBE=∠BAC﹣∠BAD,
即∠ABF=∠CAF,
∴∠ACH=∠CAF,
∴AF∥CH,
∵∠AFC=90°,∠AFE=60°,
∴CF⊥CH,∠CFH=30°,
∴FH=2CH,
∴FH=2BF,
∵FD∥CH,
∴![]() ,
,
∴BD=![]() DC.
DC.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】2020年3月20日,深圳市民中心及周邊樓宇為當日返回深圳的援鄂醫療隊員亮燈,歡迎最美逆行者回家.小洪在歡迎英雄回家現場,如圖,若他觀測到英雄畫像電子屏頂端A和底端C的仰角分別為∠α和∠β,小洪所站位置E到電子屏邊緣AC垂直地面的B點距離為m米,那么英雄畫像電子屏高AC為( )
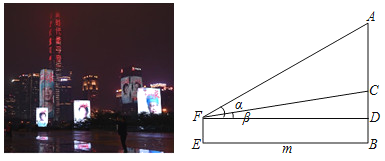
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩張完全重合的矩形紙片,將其中一張繞點![]() 順時針旋轉
順時針旋轉![]() 后得到矩形
后得到矩形![]() (如圖1),連接
(如圖1),連接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)試探究線段![]() 與線段
與線段![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
(2)把![]() 與
與![]() 剪去,將
剪去,將![]() 繞點
繞點![]() 順時針旋轉得
順時針旋轉得![]() ,邊
,邊![]() 交
交![]() 于點
于點![]() (如圖2),設旋轉角為
(如圖2),設旋轉角為![]() ,當
,當![]() 為等腰三角形時,求
為等腰三角形時,求![]() 的度數;
的度數;
(3)若將![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如圖3),
(如圖3),![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 時,求平移的距離.
時,求平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
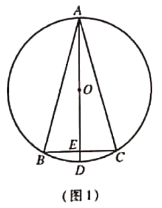
【題目】已知:![]() 是
是![]() 的內接三角形,且
的內接三角形,且![]() ,直徑
,直徑![]() 交
交![]() 于點
于點![]() .
.
![]() 如圖1 ,求證:
如圖1 ,求證:![]() ;
;
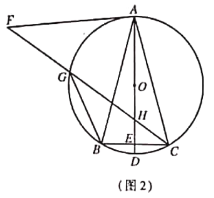
![]() 如圖2,將線段
如圖2,將線段![]() 繞點
繞點![]() 順時針旋轉得到線段
順時針旋轉得到線段![]() ,旋轉角為
,旋轉角為![]() 連接
連接![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,連接
,連接![]() ,求證:
,求證: ![]() ;
;
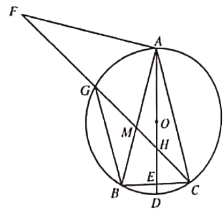
![]() 如圖3,在(2)的條件下,當
如圖3,在(2)的條件下,當![]() 時,
時,![]() 交
交![]() 于點
于點![]() 若
若![]() 求
求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】化簡:![]() +
+![]() +…+
+…+![]() .
.
為了能找到復雜計算問題的結果,我們往往會通過將該問題分解,試圖找尋算式中每個式子是否存在某種共同規律,然后借助這個規律將問題轉化為可以解決的簡單問題.下面我們嘗試著用這個思路來解決上面的問題.請你按照這個思路繼續進行下去,并把相應橫線上的空格補充完整.
(分析問題)第1個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第2個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第3個加數:![]() =
=![]() ﹣
﹣![]() ;
;
第4個加數: =![]() ﹣
﹣![]() ;
;
(總結規律)第n個加數: = ﹣ .
(解決問題)請你利用上面找到的規律,繼續化簡下面的問題.(結果只需化簡,無需求出最后得數)![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
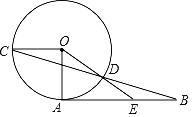
【題目】如圖,AB是⊙O的切線,OA,OC是⊙O的半徑,且OC∥AB,連接BC交⊙O于點D,點D恰為BC的中點,連接OD并延長,交AB于點E.
(1)求∠B的度數;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD與AB相交,連接CO,過點D作⊙O的切線,與AB的延長線交于點E,若DE∥AC,∠BAC=40°,則∠OCD的度數為( )
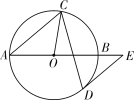
A.65°B.30°C.25°D.20°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com