(2010•南寧)2010年1月1日,全球第三大自貿區-中國-東盟自由貿易區正式成立,標志著該貿易區開始步入“零關稅”時代,廣西某民營邊貿公司要把240頓白砂糖運往東盟某國的A,B兩地,現用大,小兩種貨車共20輛,恰好能一次性裝完這批白砂糖.已知這兩種火車的載重量分別為15噸/輛和10噸/輛,運往A地的運費為:大車630元/輛,小車420元/輛;運往B地的運費為:大車750元/輛,小車550元/輛.
(1)求這兩種貨車各用多少輛;
(2)如果安排10輛貨車前往A地,其余貨車前往B地,且運往A地的白砂糖不少于115噸,請你設計出使用總運費最少的貨車調配方案,并求出最少總運費?
【答案】
分析:(1)設大車用x輛,小車用y輛,根據“大車數量+小車數量=20”“大車裝的貨物數量+小車裝的貨物數量=240噸”作為相等關系列方程組即可求解;也可列成一元一次方程求解;
(2)設總運費為W元,調往A地的大車a輛,小車(10-a)輛;調往B地的大車(8-a)輛,小車(a+2)輛,根據運費的求算方法列出關于運費的函數關系式W=10a+11300,再根據“運往A地的白砂糖不少于115噸”列關于a的不等式求出a的取值范圍,結合一次函數的單調性得出w的最小值即可求解.
解答:解:(1)解法一:設大車用x輛,小車用y輛,依據題意,得
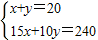
,
解得
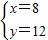
.
∴大車用8輛,小車用12輛.
解法二:設大車用x輛,小車用(20-x)輛,依據題意,得
15x+10(20-x)=240,
解得x=8.
∴20-x=20-8=12(輛).
∴大車用8輛,小車用12輛.
(2)設總運費為W元,調往A地的大車a輛,小車(10-a)輛;
調往B地的大車(8-a)輛,小車12-(10-a)=(a+2)輛,
則W=630a+420(10-a)+750(8-a)+550(a+2).
即:W=10a+11300(0≤a≤8,a為整數).
∵15a+10(10-a)≥115,
∴a≥3.
又∵W隨a的增大而增大,
∴當a=3時,w最小.
當a=3時,W=10×3+11300=11330.
因此,應安排3輛大車和7輛小車前往A地,安排5輛大車和5輛小車前往B地,最少運費為11330元.
點評:本題考查了二元一次方程組、一次函數和一元一次不等式的應用,將現實生活中的事件與數學思想聯系起來,讀懂題列出相關的式子是解題的關鍵.注意本題中所給出的相等關系和不等關系關鍵語句“現用大,小兩種貨車共20輛,恰好能一次性裝完這批白砂糖”“運往A地的白砂糖不少于115噸”等.

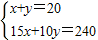 ,
,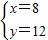 .
.

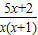 =
=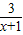 去分母,整理后得( )
去分母,整理后得( )