
【題目】如圖,在等腰![]() 中,
中,![]() ,
,![]() 是斜邊
是斜邊![]() 的中點,
的中點,![]() 交邊
交邊![]() 、
、![]() 于點
于點![]() 、
、![]() ,連結
,連結![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的面積是( )
的面積是( )
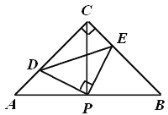
A.2B.2.5C.3D.3.5
【答案】B
【解析】
首先根據等腰直角三角形的性質和余角的性質可證明△BPE≌△CPD,可得PE=PD,于是所求的![]() 的面積即為
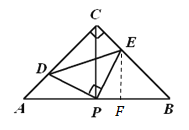
的面積即為![]() ,故只要求出PE2的值即可,可過點E作EF⊥AB于點F,如圖,根據題意可依次求出BE、BF、BP、PF的長,即可根據勾股定理求出PE2的值,進而可得答案.
,故只要求出PE2的值即可,可過點E作EF⊥AB于點F,如圖,根據題意可依次求出BE、BF、BP、PF的長,即可根據勾股定理求出PE2的值,進而可得答案.
解:在![]() 中,∵
中,∵![]() ,AC=BC,
,AC=BC,![]() 是斜邊
是斜邊![]() 的中點,
的中點,
∴AP=BP=CP,CP⊥AB,∠B=∠BCP=∠DCP=45°,
∵∠DPC+∠EPC=90°,∠BPE+∠EPC=90°,∴∠DPC=∠BPE,
在△BPE和△CPD中,∵∠B=∠DCP,BP=CP,∠BPE=∠DPC,∴△BPE≌△CPD(ASA),
∴PE=PD,
∵![]() ,
,![]() ,∴CE=1,BE=3,
,∴CE=1,BE=3,
過點E作EF⊥AB于點F,如圖,則EF=BF=![]() ,
,
又∵BP=![]() ,∴
,∴![]() ,
,
在直角△PEF中,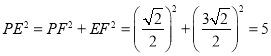 ,
,
∴![]() 的面積=
的面積=![]() .
.
故選:B.


科目:初中數學 來源: 題型:
【題目】下列命題是真命題的是( )
A.三角形的三條高線相交于三角形內一點
B.等腰三角形的中線與高線重合
C.三邊長為![]() 的三角形為直角三角形
的三角形為直角三角形
D.到線段兩端距離相等的點在這條線段的垂直平分線上
查看答案和解析>>
科目:初中數學 來源: 題型:
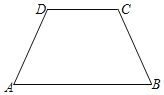
【題目】如圖,在四邊形ABCD中,AB∥DC,邊AD與BC不平行
(1)若∠A=∠B,求證:AD=BC.
(2)已知AD=BC,∠A=70°,求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
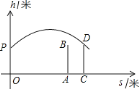
【題目】甲、乙兩人進行羽毛球比賽,甲發出一個十分關鍵的球,出手點為![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)與其飛行的水平距離
(米)與其飛行的水平距離![]() (米)之間的關系式為
(米)之間的關系式為![]() .如圖,已知球網
.如圖,已知球網![]() 距原點
距原點![]() 米,乙(用線段
米,乙(用線段![]() 表示)扣球的最大高度為
表示)扣球的最大高度為![]() 米,設乙的起跳點
米,設乙的起跳點![]() 的橫坐標為
的橫坐標為![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而導致接球失敗,則
,若乙原地起跳,因球的高度高于乙扣球的最大高度而導致接球失敗,則![]() 的取值范圍是( )
的取值范圍是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標平面內,小明站在點A(﹣10,0)處觀察y軸,眼睛距地面1.5米,他的前方5米處有一堵墻DC,若墻高DC=2米,則小明在y軸上的盲區(即OE的長度)為_____米.

查看答案和解析>>
科目:初中數學 來源: 題型:
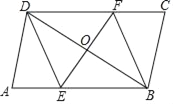
【題目】如圖所示,平行四邊形形ABCD中,過對角線BD中點O的直線分別交AB,CD邊于點E,F.
(1)求證:四邊形BEDF是平行四邊形;
(2)請添加一個條件使四邊形BEDF為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生的安全意識情況,在全校范圍內隨機抽取部分學生進行問卷調查,根據調查結果,把學生的安全意識分成“淡薄”、“一般”、“較強”、“很強”四個層次,并繪制成如圖9的兩幅尚不完整的統計圖.
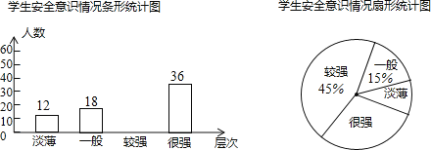
根據以上信息,解答下列問題:
(1)這次調查一共抽取了 名學生;
(2)請將條形統計圖補充完整;
(3)分別求出安全意識為“淡薄”的學生占被調查學生總數的百分比、安全意識為“很強”的學生所在扇形的圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=2,∠B=∠C=40°,點D在線段BC上運動(D不與B、C重合),連接AD,作∠ADE=40°,DE交線段AC于E.
(1)當∠BDA=115°時,∠EDC= °,∠DEC= °;點D從B向C運動時,∠BDA逐漸變 (填“大”或“小”);
(2)當DC等于多少時,△ABD≌△DCE,請說明理由;
(3)在點D的運動過程中,△ADE的形狀可以是等腰三角形嗎?若可以,請直接寫出∠BDA的度數.若不可以,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支援災區,某校愛心活動小組準備用籌集的資金購買A、B兩種型號的學習用品共1000件.已知B型學習用品的單價比A型學習用品的單價多10元,用180元購買B型學習用品的件數與用120元購買A型學習用品的件數相同.
(1)求A、B兩種學習用品的單價各是多少元?
(2)若購買這批學習用品的費用不超過28000元,則最多購買B型學習用品多少件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com