
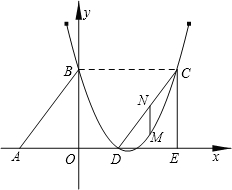
如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線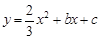 經過B點,且頂點在直線
經過B點,且頂點在直線 上.
上.
【小題1】求拋物線對應的函數關系式;
【小題2】若△DCE是由△ABO沿x軸向右平移得到的,當四邊形ABCD是菱形時,試判斷點C和點D是否在該拋物線上,并說明理由
【小題3】在(2)的條件下,連結BD,已知在對稱軸上存在一點P,使得△PBD的周長最小.請求出點P的坐標.
【小題4】在(2)、(3)的條件下,若點M是線段OB上的一個動點(與點O、B不重合),過點M作MN∥BD交x軸于點N,連結PM、PN,設OM的長為t,△PMN的面積為S,求S與t的函數關系式,并寫出自變量t的取值范圍.S是否存在最大值?若存在,求出最大值并求此時M點的坐標;若不存在,請說明理由.
【小題1】∵拋物線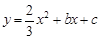 經過B(0,4),∴
經過B(0,4),∴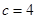 ,------1分
,------1分
∵頂點在直線 上,∴
上,∴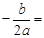
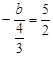 ,
, ,
,
∴所求函數關系式為: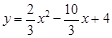 --------------------------------------2分
--------------------------------------2分
【小題2】在Rt△ABO中,OA=3,OB=4,∴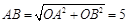 ,
,
∵四邊形ABCD是菱形,∴BC=CD=DA=AB=5,
∴C、D兩點的坐標分別是(5,4)、(2,0).---------------------------------3分
當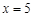 時,
時,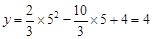 ,-----------------------------------------4分
,-----------------------------------------4分
當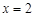 時,
時,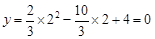 ,
,
∴點C和點D在所求拋物線上.--------------------------------------------------5分
【小題3】設CD與對稱軸交于點P,則P為所求的點, --------------------------6分
設直線CD對應的函數關系式為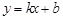 ,
,
則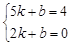 ,解得:
,解得: ,
,
∴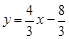 ,---------------------7分
,---------------------7分
當 時,
時,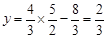 ,∴P(
,∴P(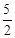 ,
,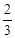 ),-------------------8分
),-------------------8分
【小題4】∵MN∥BD,∴△OMN∽△OBD,
∴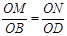 ,
, ,
,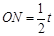 ,---------------9分
,---------------9分
設對稱軸交x軸于點F,則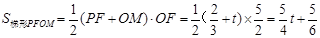 ,
,
∵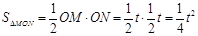 ,
,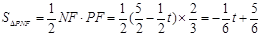 ,
,
∴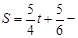
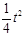
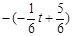
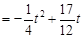 (
( -------------10分
-------------10分
由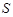
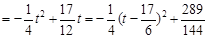 ,
,
∴當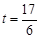 時,S取得最大值為
時,S取得最大值為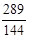 ,-----------------11分
,-----------------11分
此時點M的坐標為(0,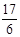 ).
).
解析


科目:初中數學 來源: 題型:
 如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=
如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| k |
| x |
 象在第四象限的交點,AB⊥x軸于B,且S△ABO=
象在第四象限的交點,AB⊥x軸于B,且S△ABO=| 5 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=
標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,Rt△ABO的頂點A是反比例函數y=
如圖,Rt△ABO的頂點A是反比例函數y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com