Question

類比聯想：既然任意一個三角形的三邊的垂直平分線交于一點，那三角形的三邊上的中線是否也交于一點；三個角的平分線是否也交于一點；試通過折紙或用直尺、圓規畫圖驗證這種猜想．

Answer 1

【答案】分析：（1）根據題意畫出圖形，設△ABC的兩條中線BD、CE相交于點G，連接AG并延長交BC于M，作BN∥CE，連接CN，由平行四邊形的判定定理可判斷出四邊形BNCG是平行四邊形，再由平行四邊形的對角線互相平分即可得出結論；
（2）根據題意畫出圖形，由角平分線的性質判斷出PF=PE即可．
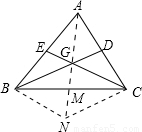
解答：解：（1）如圖，設△ABC的兩條中線BD、CE相交于點G，連接AG并延長交BC于M，作BN∥CE，連接CN，
∵E是AB的中點，BN∥CE，
∴點G是AN的中點，
∵點D是AC的中點，
∴GD∥CN，
∴四邊形BNCG是平行四邊形，
∴BC、GN互相平分，即點M是BC的中點，AM是BC的中線，即△ABC的三條中線交于一點；

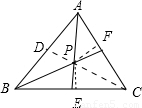
（2）如圖，△ABC中，∠A、∠B的平分線交于點P，過P作AB、BC、AC的垂線，垂足分別為D、E、F，
∵AP、BP分別為∠A、∠B的平分線，
∴PF=PD=PE，
∵PF=PE，PE⊥BC，PF⊥AC，
∴點P在∠C的平分線上，
∴三角形的三個內角的角平分線相交于一點．

點評：本題考查的是三角形的三個角平分線、三條邊的中線交于一點的證明過程，是中學階段必須掌握的知識點．