
【題目】計算: ![]() +
+ ![]() tan30°+|1﹣
tan30°+|1﹣ ![]() |﹣(﹣
|﹣(﹣ ![]() )﹣2 .
)﹣2 .
【答案】解:原式=2 ![]() +
+ ![]() ×
× ![]() +
+ ![]() ﹣1﹣4=2
﹣1﹣4=2 ![]() +1+
+1+ ![]() ﹣1﹣4=
﹣1﹣4= ![]() ﹣4
﹣4
【解析】依據二次根式的性質、特殊銳角三角函數值、絕對值的性質、負整數指數冪的性質進行化簡,然后再進行計算即可.
【考點精析】掌握整數指數冪的運算性質和特殊角的三角函數值是解答本題的根本,需要知道aman=am+n(m、n是正整數);(am)n=amn(m、n是正整數);(ab)n=anbn(n是正整數);am/an=am-n(a不等于0,m、n為正整數);(a/b)n=an/bn(n為正整數);分母口訣:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口訣:“123,321,三九二十七”.


科目:初中數學 來源: 題型:
【題目】一列快車從甲地駛往乙地,一列慢車從乙地駛往甲地,兩車同時出發,設慢車行駛的時間為x(h),兩車之間的距離為y,圖中的折線表示y與x之間的函數關系.
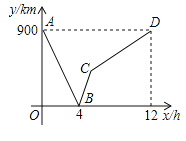
(1)甲、乙兩地之間的距離為 千米;圖中點B的實際意義是 ;
(2)求線段BC所表示的y與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)若第二列快車也從甲地出發駛往乙地,速度與第一列快車相同.在第一列快車與慢車相遇30分鐘后,第二列快車與慢車相遇.求第二列快車比第一列快車晚出發多少小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1+∠2=180°,∠DAE=∠BCF.
(1)試判斷直線AE與CF有怎樣的位置關系?并說明理由;
(2)若∠BCF=70°,求∠ADF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,BC=24,tanC=2,如果將△ABC沿直線l翻折后,點B落在邊AC的中點E處,直線l與邊BC交于點D,那么BD的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平行四邊形ABCD中,連接對角線BD,作AE⊥BD于E,CF⊥BD于F, 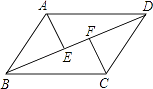
(1)求證:△AED≌△CFB;
(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四邊形ABCD的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
小明遇到這樣一個問題:
已知二次三項式x2﹣4x+m有一個因式是(x+3),求另一個因式以及m的值.
小明發現,可以設另一個因式為(x+n),得
x2﹣4x+m=(x+3)(x+n)
則x2﹣4x+m=x2+(n+3)x+3n
∴![]()
利用方程組可以解決.
請回答:
另一個因式為 ,m的值為 ;
參考小明的方法,解決下面的問題:
已知二次三項式2x2+3x﹣k有一個因式是(x﹣4),求另一個因式以及k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com