
 m2=0的兩個(gè)實(shí)數(shù)根,求證:AM=AN;
m2=0的兩個(gè)實(shí)數(shù)根,求證:AM=AN;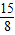 ,DN=
,DN= ,求DE的長(zhǎng);
,求DE的長(zhǎng);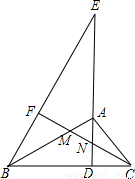
 m2)=-(m-2n)2≥0,
m2)=-(m-2n)2≥0, m2=0有兩個(gè)相等實(shí)根,
m2=0有兩個(gè)相等實(shí)根,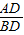 =
=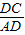 ,
, =
=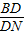 ,
,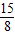 ,DN=
,DN= ,
, DE,
DE,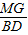 =
= ,
, =
=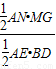 =
=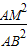 =
=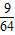 ,
,
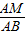 =
= ,
,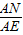 =
=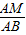 =
= ,
,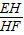 =
=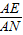 =
= ,
,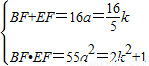 ,
,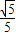 ,
,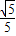 ,
,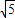 ,
, =
=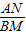 =
=
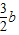 .
.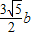
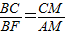 ,∴
,∴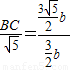 ,
,


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
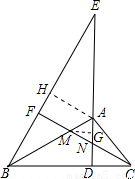
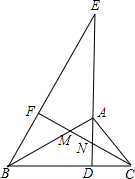 已知,如圖,AD為Rt△ABC斜邊BC上的高,點(diǎn)E為DA延長(zhǎng)線上一點(diǎn),連接BE,過(guò)點(diǎn)C作CF⊥BE于點(diǎn)F,交AB、AD于M、N兩點(diǎn).
已知,如圖,AD為Rt△ABC斜邊BC上的高,點(diǎn)E為DA延長(zhǎng)線上一點(diǎn),連接BE,過(guò)點(diǎn)C作CF⊥BE于點(diǎn)F,交AB、AD于M、N兩點(diǎn).| 5 |
| 4 |
| 15 |
| 8 |
| 9 |
| 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2013屆北京市(初中部)八年級(jí)上學(xué)期期中數(shù)學(xué)試卷(解析版) 題型:解答題
已知:如圖,AD為△ABC的內(nèi)角平分線,且AD=AB,CM⊥AD于M. 求證:AM= (AB+AC)
。
(AB+AC)
。

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com