
【題目】如圖,AD是△ABC的中線,E,F分別是AD和AD延長線上的點,且DE=DF,連接BF、CE,且∠FBD=35°,∠BDF=75°,下列說法:①△BDF≌CDE;②ABD和△ACD面積相等;③BF∥CE;④∠DEC=70°,其中正確的有( ) 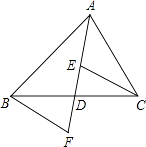
A.1個
B.2個
C.3個
D.4個
【答案】D
【解析】解:∵AD是△ABC的中線, ∴BD=CD,
∴△ABD的面積=△ACD的面積,
在△BDF和△CDE中, 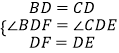 ,
,
∴△BDF≌△CDE(SAS),故①②正確
∴∠F=∠CED,∠DEC=∠F,
∴BF∥CE,故③正確,
∵∠FBD=35°,∠BDF=75°,
∴∠F=180°﹣35°﹣75°=70°,
∴∠DEC=70°,故④正確;
綜上所述,正確的是①②③④4個.
故答案為:D.
根據三角形中線的定義可得BD=CD,得出△ABD的面積=△ACD的面積,然后利用“邊角邊”證明△BDF和△CDE全等,由全等三角形的性質得出∠F=∠CED,∠DEC=∠F,再根據內錯角相等,兩直線平行可得BF∥CE,最后根據三角形內角和定理求出∠F,得出④正確,即可得出結論.


科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,AD=3,以頂點D為圓心作半徑為r的圓,若點A,B,C中至少有一個點在圓內,且至少有一個點在圓外,則r的值可以是下列選項中的( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,AB=AC,點E、F分別為邊AB、BC上的點,且AE=BF,連接CE、AF交于點H,連接DH交AG于點O.則下列結論①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正確的是( )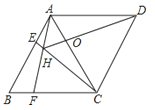
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校校門口有一個長為9m的長條形(長方形)電子顯示屏,學校的有關活動都會在“電子顯示屏”播出,由于各次活動的名稱不同,字數也就不等,為了制作及顯示時方便美觀,負責播出的老師對有關數據作出了如下規定:若字數在8個以下,邊空:字寬:字距=2:4:1;若字數在8個以上(含8個),邊空:字寬:字距=2:3:1,如圖所錄:
(1)某次活動的字數為9個,求字距是多少?
(2)如果某次活動的字寬為36cm,問字數是多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com