
【題目】如圖,已知直角梯形![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上的一動點,過
邊上的一動點,過![]() 作線段
作線段![]() 的垂直平分線,交
的垂直平分線,交![]() 于點
于點![]() ,并交射線
,并交射線![]() 于點
于點![]() .
.
(1)如圖1,當點![]() 與點
與點![]() 重合時,求
重合時,求![]() 的長;
的長;
(2)設![]() ,
,![]() ,求
,求![]() 與
與![]() 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(3)如圖2,聯結![]() ,當
,當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的長.
的長.



【答案】(1)BC=5;(2)![]() ;(3)
;(3)![]() 的長為
的長為![]() 或3或
或3或![]() .
.
【解析】
(1)根據垂直平分線性質可知![]() ,設
,設![]() ,
,![]() ,在
,在![]() 中用勾股定理求出
中用勾股定理求出![]() ,即可解答;
,即可解答;
(2)聯結![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,消去二次項即可得到
,消去二次項即可得到![]() 與
與![]() 的函數關系式;根據點
的函數關系式;根據點![]() 是
是![]() 邊上的一動點結合(1)即可得出
邊上的一動點結合(1)即可得出![]() 的定義域;
的定義域;
(3)分三種情況討論,分別畫出圖形,根據相等的邊用勾股定理列方程求解即可.
解:(1)∵梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,![]() ,設
,設![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)聯結![]() ,
,![]() ,
,
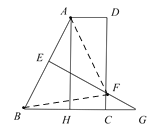
∵![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
(3)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]()
當![]() 是等腰三角形時
是等腰三角形時
①∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
②![]()
取![]() 中點
中點![]() ,聯結
,聯結![]()
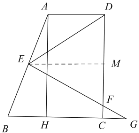
∵![]() 為
為![]() 的中點
的中點
∴![]() 為梯形中位線
為梯形中位線
∴![]()
∵![]()
∴![]() 為
為![]() 中點,
中點,
∴此時![]() 與
與![]() 重合
重合
∴![]()
③![]()
聯結![]() 并延長交
并延長交![]() 延長線于點
延長線于點![]()
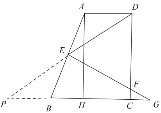
此時![]() .
.
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴在![]() 中,
中,![]() ,
,
∵![]()
∴解得![]() ,
,![]() (不合題意含去)
(不合題意含去)
∴綜上所述,當![]() 是等腰三角形時,
是等腰三角形時,![]() 的長為
的長為![]() 或3或
或3或![]()


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠BAD=25°,∠ADC=115°,O為AB的中點,以點O為圓心、AO長為半徑作圓,恰好點D在⊙O上,連接OD,若∠EAD=25°,下列說法中不正確的是( ) 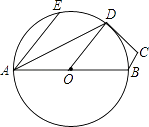
A.D是劣弧 ![]() 的中點
的中點
B.CD是⊙O的切線
C.AE∥OD
D.∠DOB=∠EAD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于三個數a,b,c,M![]() 表示a,b,c這三個數的平均數,min
表示a,b,c這三個數的平均數,min![]() 表示a,b,c這三個數中最小的數,如:
表示a,b,c這三個數中最小的數,如:
M![]() ,min
,min![]() =-1;
=-1;
M![]() ,min
,min![]() =
=![]() ;
;
解決下列問題:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min![]() =2,則x的取值范圍是______________;
=2,則x的取值范圍是______________;
(3) ①若M![]() =min
=min![]() ,那么x=______________;
,那么x=______________;
②根據①,你發現結論“若M![]() =min
=min![]() ,則______________;(填a,b,c的大小關系);
,則______________;(填a,b,c的大小關系);
③運用②解決問題:(寫出求解的過程)
若M![]() =min
=min![]() ,
,
求x+y 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了在九月份迎接高一年級的新生,決定將學生公寓樓重新裝修,現學校招用了甲、乙兩個工程隊.若兩隊合作,8天就可以完成該項工程;若由甲隊先單獨做3天后,剩余部分由乙隊單獨做需要18天才能完成.
(1)求甲、乙兩隊工作效率分別是多少?
(2)甲隊每天工資3000元,乙隊每天工資1400元,學校要求在12天內將學生公寓樓裝修完成,若完成該工程甲隊工作m天,乙隊工作n天,求學校需支付的總工資w(元)與甲隊工作天數m(天)的函數關系式,并求出m的取值范圍及w的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為3cm,動點P從B點出發以3cm/s的速度沿著邊BC﹣CD﹣DA運動,到達A點停止運動;另一動點Q同時從B點出發,以1cm/s的速度沿著邊BA向A點運動,到達A點停止運動.設P點運動時間為x(s),△BPQ的面積為y(cm2),則y關于x的函數圖象是( )
A.
B.
C.
D.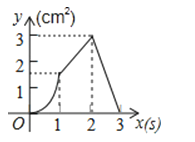
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,若△ABC和△ADE為等邊三角形,M,N分別是BE,CD的中點,
(1)求證:△AMN是等邊三角形.
(2)當把△ADE繞A點旋轉到圖2的位置時,CD=BE是否仍然成立?若成立請證明,若不成立請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用正方形硬紙板做三棱柱盒子,每個盒子由3個矩形側面和2個正三角形底面組成,硬紙板以如圖兩種方法裁剪(裁剪后邊角料不再利用)
A方法:剪6個側面;
B方法:剪4個側面和5個底面.

現有38張硬紙板,裁剪時x張用A方法,其余用B方法.
(1)用x的代數式分別表示裁剪出的側面和底面的個數;
(2)若裁剪出的側面和底面恰好全部用完,則能做多少個盒子?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com