證明:(1)根據三角形的內心是三角形的角平分線的交點以及三角形的內角和定理,得
∠ECO=

∠ACB,
設BX與AC的交點是F,則
∠EXO=180°-∠AED-∠EFX=180°-

(180°-∠A)-180°+

∠ABC+∠ACB=

∠ACB,
∴O、E、X、C四點共圓;
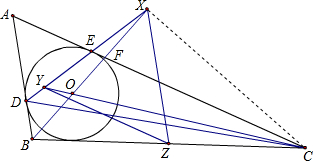
(2)證明:由切線長定理得:AE=AD,
∵∠A=60°,
∴△ADE是等邊三角形,
∴∠ADE=∠AED=60°,
∵由(1)得∠BXC=∠OEC=90°,XZ=BZ,
∴∠ZBX=∠ZXB=∠ABX,
∴XZ∥AB,
∴∠YXZ=∠ADE=60°,
同理YZ∥AC,則∠ZYX=∠AED=60°,
所以△XYZ是等邊三角形.
分析:(1)結合圖形,發現:只要能夠證明∠EXO=∠ECO即可.根據三角形的內角和定理以及三角形的內心的定義即可證明;
(2)根據切線的性質,得XE⊥AC.根據(1)中的四點共圓,得∠OXC=∠OEC=90°,再根據直角三角形斜邊上的中線等于斜邊的一半,得XZ=BZ;進而根據等邊對等角和∠ABX=∠CBX,所以得∠ABX=∠BXZ,則XZ∥AB,所以得∠YXZ=∠ADE;根據切線長定理知AD=AE,則三角形ADE是等邊三角形,則∠ADE=60°.同理∠ZYX=∠AED=60°.則可知三角形XYZ是等邊三角形.
點評:綜合運用了切線長定理、三角形的內心的性質以及直角三角形的性質和等邊三角形的判定和性質.

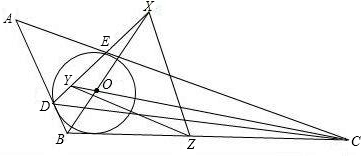 O切于點E,BO與DE交于點X,CO與DE交于點Y,點Z是BC的中點.
O切于點E,BO與DE交于點X,CO與DE交于點Y,點Z是BC的中點. ∠ACB,
∠ACB, (180°-∠A)-180°+
(180°-∠A)-180°+ ∠ABC+∠ACB=
∠ABC+∠ACB= ∠ACB,
∠ACB,


 (2012•黔東南州)如圖,⊙O是△ABC的外接圓,圓心O在AB上,過點B作⊙O的切線交AC的延長線于點D.
(2012•黔東南州)如圖,⊙O是△ABC的外接圓,圓心O在AB上,過點B作⊙O的切線交AC的延長線于點D.