
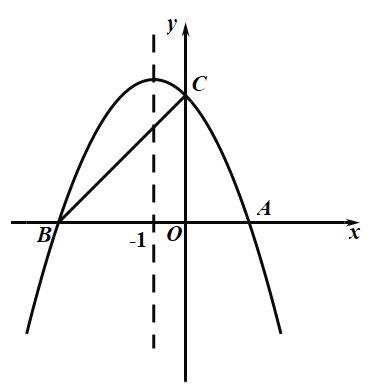
【題目】如圖,拋物線![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,它的對稱軸是直線
,它的對稱軸是直線![]() .
.
(1)求拋物線的表達式;
(2)連接![]() ,求線段
,求線段![]() 的長;
的長;
(3)若點![]() 在
在![]() 軸上,且
軸上,且![]() 為等腰三角形,請求出符合條件的所有點
為等腰三角形,請求出符合條件的所有點![]() 的坐標.
的坐標.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
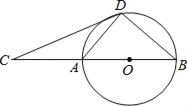
【題目】如圖,D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.
(1)求證:CD是⊙O的切線;
(2)若BC=6,tan∠CDA=![]() ,求CD的長.
,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
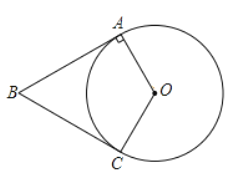
【題目】如圖,四邊形OABC中,![]() .OA=OC, BA=BC.以O為圓心,以OA為半徑作☉O
.OA=OC, BA=BC.以O為圓心,以OA為半徑作☉O
(1)求證:BC是☉O的切線:
(2)連接BO并延長交⊙O于點D,延長AO交⊙O于點E,與此的延長線交于點F若![]() .
.
①補全圖形;
②求證:OF=OB.
查看答案和解析>>
科目:初中數學 來源: 題型:
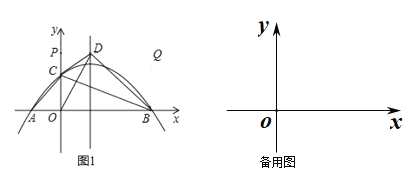
【題目】在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,將
,將![]() 沿
沿![]() 所在的直線翻折,得到
所在的直線翻折,得到![]() ,連接
,連接![]() .
.
(1)點![]() 的坐標為 ,點
的坐標為 ,點![]() 的坐標為 ;
的坐標為 ;
(2)如圖1,若點![]() 落在拋物線的對稱軸上,且在
落在拋物線的對稱軸上,且在![]() 軸上方,求拋物線的解析式.
軸上方,求拋物線的解析式.
(3)設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線分![]() 別交
別交![]() 軸、
軸、![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 于點
于點![]() .動點
.動點![]() 在直線
在直線![]() 上以每秒
上以每秒![]() 個單位的速度從點
個單位的速度從點![]() 向終點
向終點![]() 運動,同時,動點
運動,同時,動點![]() 以每秒
以每秒![]() 個單位的速度從點
個單位的速度從點![]() 沿
沿![]() 的方向運動,當點
的方向運動,當點![]() 到達終點
到達終點![]() 時,點
時,點![]() 同時停止運動.設運動時間為
同時停止運動.設運動時間為![]() 秒.
秒.
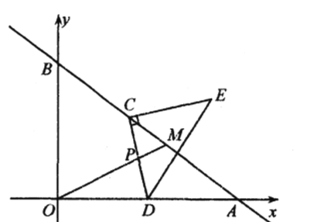
(1)求點![]() 的坐標和
的坐標和![]() 的長.
的長.
(2)當![]() 時,線段
時,線段![]() 交
交![]() 于點
于點![]() 且
且![]() 求
求![]() 的值.
的值.
(3)在點![]() 的整個運動過程中,
的整個運動過程中,
①直接用含![]() 的代數式表示點
的代數式表示點![]() 的坐標.
的坐標.
②利用(2)的結論,以![]() 為直角頂點作等腰直角
為直角頂點作等腰直角![]() (點
(點![]() 按逆時針順序排列).當
按逆時針順序排列).當![]() 與
與![]() 的一邊平行時,求所有滿足條件的
的一邊平行時,求所有滿足條件的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一期間,樂樂與小佳兩個人打算騎共享單車騎行出游,兩人打開手機![]() 進行選擇,已知附近共有3種品牌的4輛車,其中
進行選擇,已知附近共有3種品牌的4輛車,其中![]() 品牌有2輛,
品牌有2輛,![]() 品牌和
品牌和![]() 品牌各有1輛,手機上無法識別品牌,且有人選中車后其他人無法再選.
品牌各有1輛,手機上無法識別品牌,且有人選中車后其他人無法再選.
(1)若樂樂首先選擇,求樂樂選中![]() 品牌單車的概率;
品牌單車的概率;
(2)請用畫樹狀圖或列表的方法求樂樂和小佳選中同一品牌單車的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程ax2+2x﹣3=0有兩個不相等的實數根.
(1)求a的取值范圍;
(2)若此方程的一個實數根為1,求a的值及方程的另一個實數根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,一次函數![]() 的圖象與y軸交于點A,過點
的圖象與y軸交于點A,過點![]() ,且平行于x軸的直線與一次函數
,且平行于x軸的直線與一次函數![]() 的圖象,反比例函數
的圖象,反比例函數![]() 的圖象分別交于點C,D.
的圖象分別交于點C,D.
(1)求點D 的坐標(用含m的代數式表示);
(2)當m = 1時,用等式表示線段BD與CD長度之間的數量關系,并說明理由;
(3)當BD≤CD時,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果![]() 的兩個端點
的兩個端點![]() 分別在
分別在![]() 的兩邊上(不與點
的兩邊上(不與點![]() 重合),并且
重合),并且![]() 除端點外的所有點都在
除端點外的所有點都在![]() 的內部,則稱
的內部,則稱![]() 是
是![]() 的“連角弧”.
的“連角弧”.
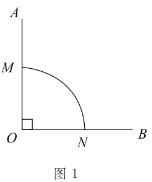
(1)圖1中,![]() 是直角,
是直角,![]() 是以
是以![]() 為圓心,半徑為1的“連角弧”.
為圓心,半徑為1的“連角弧”.
①圖中![]() 的長是______,并在圖中再作一條以
的長是______,并在圖中再作一條以![]() 為端點、長度相同的“連角弧”;
為端點、長度相同的“連角弧”;
②以![]() 為端點,弧長最長的“連角弧”的長度是_______.
為端點,弧長最長的“連角弧”的長度是_______.
(2)如圖2,在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() 在
在![]() 軸正半軸上,若
軸正半軸上,若![]() 是半圓,也是
是半圓,也是![]() 的“連角弧”,求
的“連角弧”,求![]() 的取值范圍.
的取值范圍.

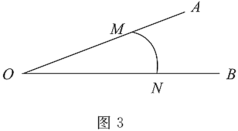
(3)如圖3,已知點![]() 分別在射線
分別在射線![]() 上,
上,![]() 是
是![]() 的“連角弧”,且
的“連角弧”,且![]() 所在圓的半徑為
所在圓的半徑為![]() ,直接寫出
,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com