
【題目】如圖1,已知![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)求證:![]() ;
;
(2)如圖2,若![]() ,
,![]() ,折疊紙片,使點
,折疊紙片,使點![]() 與點
與點![]() 重合,折痕為
重合,折痕為![]() ,且
,且![]() .
.
①求證:![]() ;
;
②點![]() 是線段
是線段![]() 上一點,連接
上一點,連接![]() ,一動點
,一動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以每秒1個單位的速度運動到點
以每秒1個單位的速度運動到點![]() ,再沿線段
,再沿線段![]() 以每秒
以每秒![]() 個單位的速度運動到
個單位的速度運動到![]() 后停止,點
后停止,點![]() 在整個運動過程中用時最少多少秒?
在整個運動過程中用時最少多少秒?
【答案】(1)見詳解;(2)①見詳解;②![]() .
.
【解析】
(1)直接利用AAS,即可證明結論成立;
(2)①由折疊的性質,得到BE=DE,EF平分∠BED,由DE⊥BC,得到∠DBE=∠ACB=∠FEB=45°,即可得到EF∥AC;
②當點Q是EF與BD的交點時,點![]() 在整個運動過程中用時最少;連接AQ、AD,可得△ADQ是等腰直角三角形,根據勾股定理求出BD,然后得到BQ=DQ=
在整個運動過程中用時最少;連接AQ、AD,可得△ADQ是等腰直角三角形,根據勾股定理求出BD,然后得到BQ=DQ=![]() ,然后求出AQ,即可求出點P運動所用的時間.
,然后求出AQ,即可求出點P運動所用的時間.
解:(1)由題意,
∵![]() ,
,![]() ,BC=CB,
,BC=CB,
∴![]() (AAS);
(AAS);
(2)①如圖:
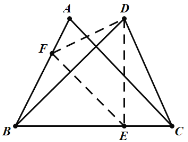
由折疊的性質,得到BE=DE,∠BEF=∠DEF,
∵DE⊥BC,
∴∠BED=90°,
∴∠BEF=∠DEF=∠DBE=∠BDE=45°;
∵![]() ,
,
∴∠ACB=∠DBE,
∴∠ACB=∠DBE=∠FEB=45°,
∴EF∥AC;
②如圖,連接AQ交BC于點H,連接AD,當點Q是EF與BD的交點時,點![]() 在整個運動過程中用時最少;
在整個運動過程中用時最少;
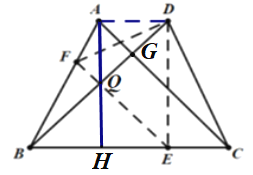
此時AQ∥DE,AD∥BC,
∴∠ADQ=45°,∠DAQ=90°,
∴△ADQ是等腰直角三角形,
∴AD=AQ,
∵點Q時BD中點,
∴點H是BE的中點,
∵BE=DE=![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,
∴點P運動所用的時間為:
![]() (秒).
(秒).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
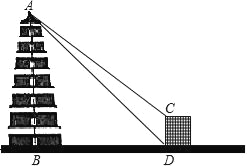
【題目】小雁塔位于唐長安城安仁坊(今陜西省西安市南郊)薦福寺內,又稱“薦福寺塔”,建于唐景龍年間,與大雁塔同為唐長安城保留至今的重要標志.小明在學習了銳角三角函數后,想利用所學知識測量“小雁塔”的高度,小明在一棟高9.982米的建筑物底部D處測得塔頂端A的仰角為45°,接著在建筑物頂端C處測得塔頂端A的仰角為37.5°.已知AB⊥BD,CD⊥BD,請你根據題中提供的相關信息,求出“小雁塔”的高AB的長度(結果精確到1米)(參考數據:sin37.5°≈0.61,cos37.5°≈0.79,tan37.5°≈0.77)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個長為4cm,寬為3cm的長方形木板在桌面上做無滑動的翻滾(順時針方向),木板點A位置的變化為A→Al→A2,其中第二次翻滾被面上一小木塊擋住,使木板與桌面成30°的角,則點A滾到A2位置時共走過的路徑長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
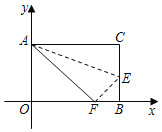
【題目】如圖,長方形AOBC,以O為坐標原點,OB、OA分別在x軸、y軸上,點A的坐標為(0,8),點B的坐標為(10,0),點E是BC邊上一點,把長方形AOBC沿AE翻折后,C點恰好落在x軸上點F處.
(1)求點E、F的坐標;
(2)求AF所在直線的函數關系式;
(3)在x軸上求一點P,使△PAF成為以AF為腰的等腰三角形,請直接寫出所有符合條件的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地農民一直保持著冬種油菜的習慣,利用農閑冬種一季油菜該地農業部門對2017年的油菜籽的生產成本、市場價格、種植面積和產量等進行了統計,并繪制了如下的統計表與統計圖(如圖):

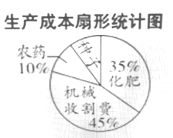
請根據以上信息解答下列問題:
(1)種植每畝油菜所需種子的成本是多少元?
(2)農民冬種油菜每畝獲利多少元?
(3)2017年該地全縣農民冬種油菜的總獲利是多少元?(結果用科學記數法表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖像
的圖像![]() 分別與
分別與![]() 、
、![]() 軸交于
軸交于![]() 兩點,正比例函數的圖像
兩點,正比例函數的圖像![]() 與
與![]() 交于點
交于點![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)在坐標軸上找一點![]() ,使以
,使以![]() 為腰的
為腰的![]() 為等腰三角形,請直接寫出點
為等腰三角形,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將一個點(橫坐標與縱坐標不相等)的橫坐標與縱坐標互換后得到的點叫做這個點的“互換點”,如(-3,5)與(5,-3)是一對“互換點”。
(1)任意一對“互換點”________(填“都能”或“都不能”)在一個反比例函數的圖象上;
(2)M、N是一對“互換點”,若點M的坐標為(2,-5),求直線MN的表達式;
(3)在拋物線![]() 的圖象上有一對“互換點”A、B,其中點A在反比例函數
的圖象上有一對“互換點”A、B,其中點A在反比例函數![]() 的圖象上,直線AB經過點P(
的圖象上,直線AB經過點P(![]() ,
,![]() ),求此拋物線的表達式.
),求此拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形![]() 置于平面直角坐標系
置于平面直角坐標系![]() 中,
中,![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標為
的坐標為![]() ,對角線
,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 是第一象限內一點.
是第一象限內一點.
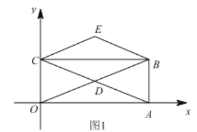
(1)如圖1,若![]() ,
,![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
(2)如圖2,當點![]() 使得
使得![]() 時,求證:
時,求證:![]() ;
;
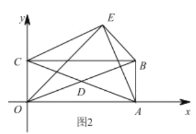
(3)在(2)的條件下,如果![]() 與
與![]() 恰好相等,求點
恰好相等,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
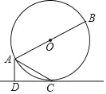
【題目】已知:如圖,AB為⊙O的直徑,AC是⊙O的弦,AD垂直于過點C的直線DC,垂足為點D,且AC平分∠BAD.
(1)求證:CD是⊙O的切線;
(2)若AD=1,AB=5,求AC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com