Question

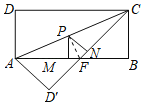
【題目】如圖，長方形ABCD中，AB＝6，AC＝3，將△ADC沿AC折疊，點D落在點D′處，CD′與AB交于點F．點P為線段AC（不含點A、C）上任意一點，PM⊥AB于點M，PN⊥CD′于點N，PM+PN＝_____．

Answer 1

【答案】3

【解析】

根據矩形的性質和翻折變換的性質得到AF＝CF，設AF＝x，根據勾股定理列出方程，解方程即可求出AF，再根據三角形的面積公式解答即可．

解：連接PF，如圖所示：

∵四邊形ABCD是矩形

∴∠B＝90°，AB∥CD，

∴BC＝＝＝3，∠DCA＝∠BAC，

∵矩形沿AC折疊，點D落在點E處，

∴△ACD≌△ACE，

∴∠DCA＝∠ECA，

∴∠BAC＝∠ECA，

∴AF＝CF，

設AF＝CF＝x，則BF＝6﹣x，

在Rt△BCF中，根據勾股定理得：BC2+BF2＝CF2，

即32+（6﹣x）2＝x2，

解得：x＝，

∴AF＝

∴S△ACF＝AFBC＝××3＝，

∵×AF×PM+×CF×PN＝S△ACF＝，

∴××（PM+PN）＝，

∴PM+PN＝3；

故答案為：3．