
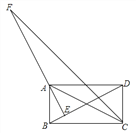
【題目】如圖,矩形ABCD中,AE⊥BD于點E,CF平分∠BCD,交EA的延長線于點F,且BC=4,CD=2,給出下列結論:①∠BAE=∠CAD;②∠DBC=30°;③AE=![]() ;④AF=
;④AF=![]() ,其中正確的是______.(填寫所有正確結論的序號)
,其中正確的是______.(填寫所有正確結論的序號)
【答案】①③④
【解析】分析:根據余角的性質得到∠BAE=∠ADB,等量代換得到∠BAE=∠CAD,故①正確;根據三角函數的定義得到tan∠DBC=![]() =
=![]() ,于是得到∠DBC≠30°,故②錯誤;由勾股定理得到BD=
,于是得到∠DBC≠30°,故②錯誤;由勾股定理得到BD=![]() =2
=2![]() ,根據相似三角形的性質得到AE=
,根據相似三角形的性質得到AE=![]() ;故③正確;根據角平分線的定義得到∠BCF=45°,求得∠ACF=45°﹣∠ACB,推出∠EAC=2∠ACF,根據外角的性質得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根據等腰三角形的判定得到AF=AC,于是得到AF=2
;故③正確;根據角平分線的定義得到∠BCF=45°,求得∠ACF=45°﹣∠ACB,推出∠EAC=2∠ACF,根據外角的性質得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根據等腰三角形的判定得到AF=AC,于是得到AF=2![]() ,故④正確.
,故④正確.
詳解:在矩形ABCD中,∵∠BAD=90°.∵AE⊥BD,∴∠AED=90°,∴∠ADE+∠DAE=∠DAE+∠BAE=90°,∴∠BAE=∠ADB.∵∠CAD=∠ADB,∴∠BAE=∠CAD,故①正確;
∵BC=4,CD=2,∴tan∠DBC=![]() =
=![]() ,∴∠DBC≠30°,故②錯誤;
,∴∠DBC≠30°,故②錯誤;
∵BD=![]() =2
=2![]() .∵AB=CD=2,AD=BC=4.∵△ABE∽△DBA,∴
.∵AB=CD=2,AD=BC=4.∵△ABE∽△DBA,∴![]() ,即
,即![]() ,∴AE=
,∴AE=![]() ;故③正確;
;故③正確;
∵CF平分∠BCD,∴∠BCF=45°,∴∠ACF=45°﹣∠ACB.∵AD∥BC,∴∠DAC=∠BAE=∠ACB,∴∠EAC=90°﹣2∠ACB,∴∠EAC=2∠ACF.∵∠EAC=∠ACF+∠F,∴∠ACF=∠F,∴AF=AC.∵AC=BD=2![]() ,∴AF
,∴AF![]() ,故④正確;
,故④正確;
故答案為:①③④.


科目:初中數學 來源: 題型:
【題目】甲、乙兩公司同時銷售一款進價為40元/千克的產品.圖①中折線ABC表示甲公司銷售價y1(元/千克)與銷售量x(千克)之間的函數關系,圖②中拋物線表示乙公司銷售這款產品獲得的利潤y2(元)與銷售量x(千克)之間的函數關系.


(1)分別求出圖①中線段AB、圖②中拋物線所表示的函數表達式;
(2)當該產品銷售量為多少千克時,甲、乙兩公司獲得的利潤的差最大?最大值為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
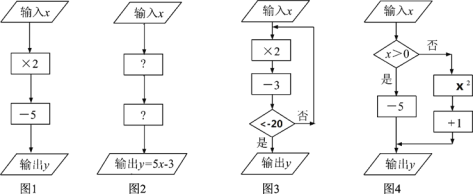
【題目】(知識背景)在學習計算框圖時,可以用![]() 表示數據輸入、輸出框;
表示數據輸入、輸出框;![]() 用表示數據處理和運算框:用◇表示數據判斷框(根據條件決定執行兩條路徑中的某一條)
用表示數據處理和運算框:用◇表示數據判斷框(根據條件決定執行兩條路徑中的某一條)
(嘗試解決)
(1)①如圖1,當輸入數![]() 時,輸出數y=_________;
時,輸出數y=_________;
②如圖2,第一個“![]() ”內,應填_________;第二個“
”內,應填_________;第二個“![]() ”內,應填_________;
”內,應填_________;
(2)①如圖3,當輸入數![]() 時,輸出數
時,輸出數![]() =_________;
=_________;
②如圖4,當輸出的值![]() =26,則輸入的值
=26,則輸入的值![]() =_________;
=_________;
(實際應用)
(3)為鼓勵節約用水,決定對用水實行“階梯價”:當每月用水量不超過10噸時(含10噸),以3元/噸的價格收費;當每月用水量超過10噸時,超過部分以4元/噸的價格收費.請設計出一個“計算框圖”,使得輸入數為用水量![]() ,輸出數為水費
,輸出數為水費![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一只不透明的口袋里裝有只有顏色不同的黑、白兩種顏色的球共20個,某學習小組做摸球實驗,將球攪勻后從中隨機摸出一個球記下顏色,然后把它放回袋中,不斷重復,下表是活動進行中的一組統計數據:
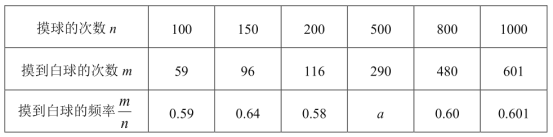
(1)上表中的a= ;
(2)“摸到白球”的概率的估計值是 (精確到0.1)
(3)試估算口袋中黑、白兩種顏色的球各有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級共有800名學生,準備調查他們對“低碳”知識的了解程度.
(1)在確定調查方式時,團委設計了以下三種方案:
方案一:調查七年級部分女生;
方案二:調查七年級部分男生;
方案三:到七年級每個班去隨機調查一定數量的學生.
請問其中最具有代表性的一個方案是 ;
(2)團委采用了最具有代表性的調查方案,并用收集到的數據繪制出兩幅不完整的統計圖(如圖①、圖②所示),請你根據圖中信息,將兩個統計圖補充完整;

(3)在扇形統計圖中,“比較了解”所在扇形的圓心角的度數是 .
(4)請你估計該校七年級約有 名學生比較了解“低碳”知識.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 、
、![]() 在數軸上分別表示有理數
在數軸上分別表示有理數![]() ,
,![]() ;
;
(1)對照數軸填寫下表:
| 6 | -1 | -2 | 4 |
| 4 | -5 | 3 | -4 |
|
(2)若![]() 、
、![]() 兩點間的距離記為
兩點間的距離記為![]() ,試問:
,試問:![]() 和
和![]() ,
,![]() 有何數量關系?
有何數量關系?
(3)寫出所有符合條件的整數點![]() ,使它到10和-10的距離之和為span>20,并求所有這些整數的數的和;
,使它到10和-10的距離之和為span>20,并求所有這些整數的數的和;
(4)找出(3)中滿足到10和-10的距離之差大于1而小于5的整數的點![]() ;
;
(5)若點![]() 表示的數為
表示的數為![]() ,當點
,當點![]() 在什么位置時,
在什么位置時,![]() 取得的值最小,并求出這個最小值.
取得的值最小,并求出這個最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為![]() 的正方形四個角上,分別剪去大小相等的等腰直角三角形,當三角形的直角邊由小變大時,陰影部分的面積也隨之發生變化,它們的變化情況如下:
的正方形四個角上,分別剪去大小相等的等腰直角三角形,當三角形的直角邊由小變大時,陰影部分的面積也隨之發生變化,它們的變化情況如下:
三角形的直角邊長/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
陰影部分的面積/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在這個變化過程中,自變量、因變量各是什么?
(2)請將上述表格補充完整;
(3)當等腰直角三角形的直角邊長由![]() 增加到
增加到![]() 時,陰影部分的面積是怎樣變化的?
時,陰影部分的面積是怎樣變化的?
(4)設等腰直角三角形的直角邊長為![]() ,圖中陰影部分的面積為
,圖中陰影部分的面積為![]() ,寫出
,寫出![]() 與
與![]() 的關系式.
的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織部分師生從學校(A地)到300千米外的B地進行紅色之旅(革命傳統教育),租用了客運公司甲、乙兩輛車,其中乙車速度是甲車速度的![]() ,兩車同時從學校出發,以各自的速度勻速行駛,行駛2小時后甲車到達服務區C地,此時兩車相距40千米,甲車在服務區休息15分鐘戶按原速度開往B地,乙車行駛過程中未做停留.
,兩車同時從學校出發,以各自的速度勻速行駛,行駛2小時后甲車到達服務區C地,此時兩車相距40千米,甲車在服務區休息15分鐘戶按原速度開往B地,乙車行駛過程中未做停留.
(1)求甲、乙兩車的速度?
(2)問甲車在C地結束休息后再行駛多長時間,甲、乙兩車相距30千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,對角線AC=6,BD=8,M、N分別是BC、CD上的動點,P是線段BD上的一個動點,則PM+PN的最小值是( )
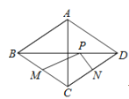
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com