
 =
= ,
, =
=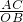 =
=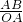 =
= ,
, ,BC=5,
,BC=5, ,AC=2
,AC=2 ,
, AB•AC=5
AB•AC=5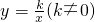 .
.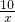 .
.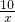 圖象上,且在第一象限內(nèi)的點(diǎn),
圖象上,且在第一象限內(nèi)的點(diǎn), ),m>0且m≠5
),m>0且m≠5 ),
),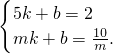 解得
解得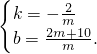
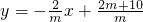 (m>0且m≠5).
(m>0且m≠5).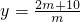 ,當(dāng)y=0時,x=5+m.
,當(dāng)y=0時,x=5+m.
 (5+m)
(5+m) -
- •m•
•m• -
- ×1×2-
×1×2- (4+m)•
(4+m)•
 -1
-1 ,由△ABC∽△OAB,可得點(diǎn)C(5,2);
,由△ABC∽△OAB,可得點(diǎn)C(5,2); ,AC=2
,AC=2 ,再求出△ABC的面積,設(shè)這個反比例函數(shù)關(guān)系式為
,再求出△ABC的面積,設(shè)這個反比例函數(shù)關(guān)系式為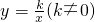 .
.


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖所示,已知一次函數(shù)y1=kx+b的圖象經(jīng)過A(1,2)、B(-1,0)兩點(diǎn),y2=mx+n的圖象經(jīng)過A、C(3,0)兩點(diǎn),則不等式組0<kx+b<mx+n的解集是( )
如圖所示,已知一次函數(shù)y1=kx+b的圖象經(jīng)過A(1,2)、B(-1,0)兩點(diǎn),y2=mx+n的圖象經(jīng)過A、C(3,0)兩點(diǎn),則不等式組0<kx+b<mx+n的解集是( )查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| k |
| x+k |
| b |
| x-b |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com