
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() ,
,![]() 軸分別相交于點
軸分別相交于點![]() 、
、![]() ,與直線
,與直線![]() 交于點
交于點![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
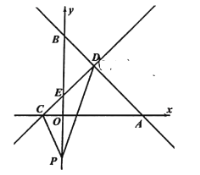
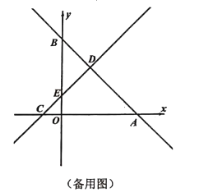
(1)若點![]() 是
是![]() 軸上一動點,連接
軸上一動點,連接![]() 、
、![]() ,求當
,求當![]() 取最大值時,
取最大值時,![]() 點的坐標;
點的坐標;
(2)在(1)問的條件下,將![]() 沿
沿![]() 軸平移,在平移的過程中,直線
軸平移,在平移的過程中,直線![]() 交直線
交直線![]() 于點
于點![]() ,則當
,則當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的長.
的長.
【答案】(1)P點坐標為![]() ;(2)BM的長為
;(2)BM的長為![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)將D點坐標代入![]() 求出m的值,然后求出C點坐標,作C點關于y軸的對稱點C',連接DC',與y軸的交點即為點P,求出DC'直線解析式,即可求出P點坐標;
求出m的值,然后求出C點坐標,作C點關于y軸的對稱點C',連接DC',與y軸的交點即為點P,求出DC'直線解析式,即可求出P點坐標;
(2)將![]() 代入直線
代入直線![]() ,求出b的值,再求A點坐標,設M點坐標為
,求出b的值,再求A點坐標,設M點坐標為![]() ,分三種情況討論:①PA=PM,②PM=AM,③PA=AM,分別求出BM的長即可.
,分三種情況討論:①PA=PM,②PM=AM,③PA=AM,分別求出BM的長即可.
(1)將![]() 代入
代入![]() 得:
得:![]()
∴![]()
當y=0時,![]() ,解得
,解得![]()
∴![]()
則![]() 關于y軸的對稱點
關于y軸的對稱點![]()
∴PC=PC',![]()
當P,C',D共線時,![]() 取得的最大值,如圖所示,
取得的最大值,如圖所示,
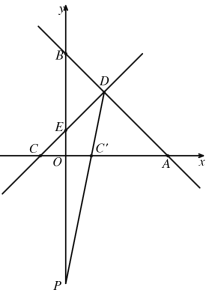
設直線PD解析式為![]() ,
,
將![]() ,
,![]() 代入得:
代入得:![]()
解得![]()
∴直線PD解析式為![]()
當x=0時,![]() ,
,
∴P點坐標為![]()
(2)將![]() 代入直線
代入直線![]() 得:
得:![]() ,
,
解得![]()
∴直線AB解析式為![]()
當y=0時,![]() ,解得
,解得![]() ,當x=0時,y=8
,當x=0時,y=8
∴A點坐標為![]() ,B點坐標為
,B點坐標為![]()
設M點坐標為![]()
①當PA=PM時,如圖所示,
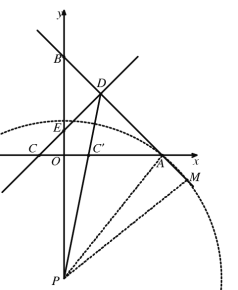
則![]()
解得![]() 或
或![]() (舍去)
(舍去)
此時M![]()
BM=![]()
②當PM=AM時,
則![]()
解得![]()
此時![]()
BM=![]()
③當PA=AM時,如圖所示,
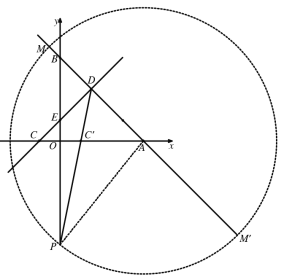
∵AB=![]() ,AM=AM'=PA=
,AM=AM'=PA=![]()
∴BM=AM-AB=![]() ,BM'=AM'+AB=
,BM'=AM'+AB=![]()
綜上可得,BM的長為![]() 或
或![]() 或
或![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】一個長為4cm,寬為3cm的長方形木板在桌面上做無滑動的翻滾(順時針方向),木板點A位置的變化為A→Al→A2,其中第二次翻滾被面上一小木塊擋住,使木板與桌面成30°的角,則點A滾到A2位置時共走過的路徑長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將一個點(橫坐標與縱坐標不相等)的橫坐標與縱坐標互換后得到的點叫做這個點的“互換點”,如(-3,5)與(5,-3)是一對“互換點”。
(1)任意一對“互換點”________(填“都能”或“都不能”)在一個反比例函數的圖象上;
(2)M、N是一對“互換點”,若點M的坐標為(2,-5),求直線MN的表達式;
(3)在拋物線![]() 的圖象上有一對“互換點”A、B,其中點A在反比例函數
的圖象上有一對“互換點”A、B,其中點A在反比例函數![]() 的圖象上,直線AB經過點P(
的圖象上,直線AB經過點P(![]() ,
,![]() ),求此拋物線的表達式.
),求此拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形![]() 置于平面直角坐標系
置于平面直角坐標系![]() 中,
中,![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標為
的坐標為![]() ,對角線
,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 是第一象限內一點.
是第一象限內一點.
(1)如圖1,若![]() ,
,![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
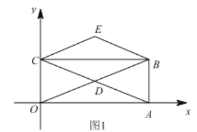
(2)如圖2,當點![]() 使得
使得![]() 時,求證:
時,求證:![]() ;
;
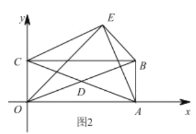
(3)在(2)的條件下,如果![]() 與
與![]() 恰好相等,求點
恰好相等,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個三角形的所有頂點都在網格的格點上,那么這個三角形叫做格點三角形,請在下列給定網格中按要求解答下面問題:
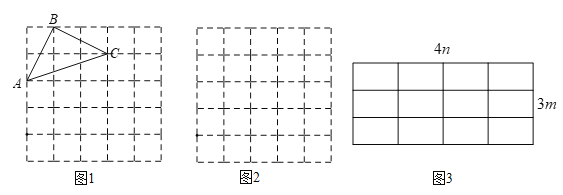
(1)直接寫出圖1方格圖(每個小方格邊長均為1)中格點△ABC的面積;
(2)已知△A1B1C1三邊長分別為![]() 、
、![]() 、
、![]() ,在圖2方格圖(每個小方格邊長均為1)中畫出格點△A1B1C1;
,在圖2方格圖(每個小方格邊長均為1)中畫出格點△A1B1C1;
(3)已知△A2B2C2三邊長分別為![]() 、
、![]() 、
、 ![]() (m>0,n>0,且m≠n)在圖3所示4n×3m網格中畫出格點△A2B2C2,并求其面積.
(m>0,n>0,且m≠n)在圖3所示4n×3m網格中畫出格點△A2B2C2,并求其面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
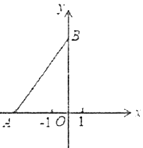
【題目】如圖,在平面直角坐標系中,點![]() ,為
,為![]() 軸負半軸上一點,點
軸負半軸上一點,點![]() 為
為![]() 軸正半軸上一點,其中
軸正半軸上一點,其中![]() 滿足方程
滿足方程![]() .
.
(1)求點![]() 、
、![]() 的坐標;
的坐標;
(2)點![]() 為
為![]() 軸負半軸上一點,且
軸負半軸上一點,且![]() 的面積為
的面積為![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 的面積等于
的面積等于![]() 的面積的一半,若存在,求出相應的
的面積的一半,若存在,求出相應的![]() 點的坐標,若不存在,請說明理由.
點的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
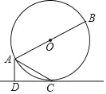
【題目】已知:如圖,AB為⊙O的直徑,AC是⊙O的弦,AD垂直于過點C的直線DC,垂足為點D,且AC平分∠BAD.
(1)求證:CD是⊙O的切線;
(2)若AD=1,AB=5,求AC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com