
【題目】已知![]() ,射線
,射線![]() 分別和直線
分別和直線![]() 交于點
交于點![]() ,射線
,射線![]() 分別和直線
分別和直線![]() 交于點
交于點![]() .點
.點![]() 在
在![]() 上(
上(![]() 點與
點與![]() 三點不重合).連接
三點不重合).連接![]() .請你根據題意畫出圖形并用等式直接寫出
.請你根據題意畫出圖形并用等式直接寫出![]() 、
、![]() 、
、![]() 之間的數量關系.
之間的數量關系.
科目:初中數學 來源: 題型:
【題目】如圖,M是△ABC的邊BC的中點,AN平分∠BAC,BN⊥AN于點N,延長BN交AC于點D,已知AB=10,BC=15,MN=3

(1)求證:BN=DN;
(2)求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)(方法回顧)證明:三角形中位線定理.
已知:如圖1,![]() 中,D、E分別是AB、AC的中點.
中,D、E分別是AB、AC的中點.
求證:![]() ,
,![]() .
.
證明:如圖1,延長DE到點F,使得![]() ,連接CF;
,連接CF;
請繼續完成證明過程;

(2)(問題解決)
如圖2,在矩形ABCD中,E為AD的中點,G、F分別為AB、CD邊上的點,若![]() ,
,![]() ,
,![]() ,求GF的長.
,求GF的長.
(3)(思維拓展)
如圖3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E為AD的中點,G、F分別為AB、CD邊上的點,若
,E為AD的中點,G、F分別為AB、CD邊上的點,若![]() ,
,![]() ,
,![]() ,求GF的長.
,求GF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個長方形運動場被分隔成A,B,A,B,C共5個區,A區是邊長為a m的正方形,C區是邊長為c m的正方形.
(1)列式表示每個B區長方形場地的周長,并將式子化簡;
(2)列式表示整個長方形運動場的周長,并將式子化簡;
(3)如果a=40,c=10,求整個長方形運動場的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一條直線過點![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() 兩點,其中點
兩點,其中點![]() 的橫坐標是
的橫坐標是![]() .
.
⑴求這條直線的函數關系式及點![]() 的坐標 ;
的坐標 ;
⑵在![]() 軸上是否存在點
軸上是否存在點![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出點
是直角三角形?若存在,求出點![]() 的坐標,若不存在,請說明理由;
的坐標,若不存在,請說明理由;
⑶過線段![]() 上一點
上一點![]() ,作
,作![]() ∥
∥![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,點
,點![]() 在第一象限;點
在第一象限;點![]() ,當點
,當點![]() 的橫坐標為何值時,
的橫坐標為何值時, ![]() 的長度最大?最大值是多少?
的長度最大?最大值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
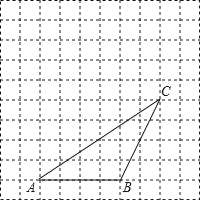
【題目】如圖,網格中每個小正方形邊長為1,△ABC的頂點都在格點(網格線的交點)上.將△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)請在圖中畫出平移后的△A′B′C′;
(2)畫出平移后的△A′B′C′的中線B′D′;
(3)若連接BB′,CC′,則這兩條線段的關系是_______;
(4)△ABC的面積為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() ,
,![]() ,
,![]() ,
,![]() .把一條長為2019個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在點A處,并按A-B-C-D-A…的規律繞在四邊形ABCD的邊上,則細線另一端所在位置的點的坐標是__________.
.把一條長為2019個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在點A處,并按A-B-C-D-A…的規律繞在四邊形ABCD的邊上,則細線另一端所在位置的點的坐標是__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備租用一批汽車,現有甲、乙兩種客車,甲種客車每輛載客量45人,乙種客車每輛載客量30人.已知1輛甲種客車和3輛乙種客車共需租金1240元,3輛甲種客車和2輛乙種客車共需租金1760元.求1輛甲種客車和1輛乙種客車的租金分別是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“國慶”期間,某電影院裝修后重新開業,試營業期間統計發現,影院每天售出的電影票張數y(張)與電影票售價![]() (元/張)之間滿足一次函數關系:
(元/張)之間滿足一次函數關系: ![]() ,
, ![]() 是整數,影院每天運營成本為1600元,設影院每天的利潤為w(元)(利潤=票房收入
是整數,影院每天運營成本為1600元,設影院每天的利潤為w(元)(利潤=票房收入![]() 運營成本).
運營成本).
(1)試求w與![]() 之間的函數關系式;
之間的函數關系式;
(2)影院將電影票售價定為多少時,每天獲利最大?最大利潤是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com