
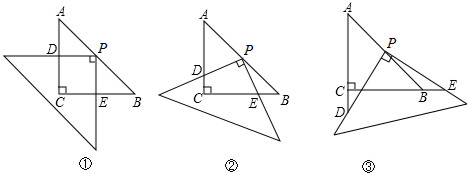
操作:在△ABC中,AC=BC=2,∠C=90°,將一塊等腰直角三角板的直角頂點放在 斜邊AB的中點P處,
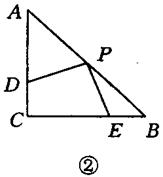
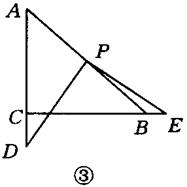
斜邊AB的中點P處, 將三角板繞點P旋轉,三角板的兩直角邊分別交射線AC、CB于D、E兩點,如圖3-1-13①②③是旋轉三角板得到的圖形中的3種情況,
將三角板繞點P旋轉,三角板的兩直角邊分別交射線AC、CB于D、E兩點,如圖3-1-13①②③是旋轉三角板得到的圖形中的3種情況,
由①②③研究:(1)三角板繞點P旋轉,觀察線段PD和PE之間有什么數量關系?并結合圖①加以證明。
(2)三角板繞點P旋轉,△PBE是否能成為等腰三角形?若能,指出所有情況(即寫出△PBE為等腰三角形時CE的長;若不能,請說明理由)。
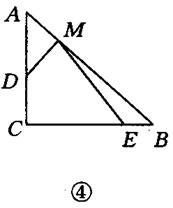
(3)若將三角板的直角頂點放在斜邊AB上的M處,且AM:MB=1:3,和前面一樣操作,試問線段MD和ME之間有什么數量關系?并結合圖④加以證明。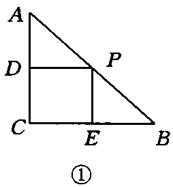
解:(1)連接PC,因為△ABC是等腰直角三角形,P是AB的中點,所以CP=PB,CP⊥AB,∠ACP=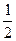 ∠ACP=45°,即∠ACP=∠B=45°,又因為∠DPC+∠CPE=∠BPE+∠CPE=90°,
∠ACP=45°,即∠ACP=∠B=45°,又因為∠DPC+∠CPE=∠BPE+∠CPE=90°,
所以∠DPC=∠BPE,即△PCD≌△PBE,所以PD=PE。…………………3分
(2)共有四種情況:①當點C與點E重合,即CE=0時,PE=PB,②當CE=2-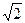 時,此時PB=BE;③當CE=1時,此時PE=BE;④當E在CB的延長線上,且CE=2+
時,此時PB=BE;③當CE=1時,此時PE=BE;④當E在CB的延長線上,且CE=2+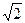 時,此時PB=EB。…6分
時,此時PB=EB。…6分
(3)MD:ME=1:3,…………………7分
證明如下:過點M作MF⊥AC,MH⊥BC,垂足分別是F、H,所以MH∥AC,MF∥BC,即四邊形CFMH是平行四邊形,因為∠C=90°,所以□CFMH是矩形,即∠FMH=90°,M F=CH,因為
F=CH,因為 ,
,
而HB=MH,所以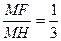 …………………9分,
…………………9分,
因為∠DMF+∠DMH=∠DMH+∠EMH=90°,所以∠DMF=∠EMH,因為∠MFD=∠EMH=90°,所以△MDF∽△MEH,即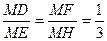 …………………10分
…………………10分
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com