
【題目】在平面直角坐標系中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,且
,且![]() .
.
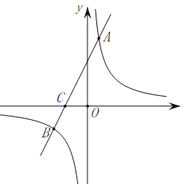
(1)求該反比例函數和一次函數的解析式;
(2)求點![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 有最大值,如果存在,請求出點
有最大值,如果存在,請求出點![]() 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
【答案】(1)反比例函數表達式為:![]() ;一次函數的表達式為:
;一次函數的表達式為:![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() 點坐標為
點坐標為![]() .
.
【解析】
(1)先過點A作AD⊥x軸,根據tan∠ACO=2,求得點A的坐標,進而根據待定系數法計算兩個函數解析式;
(2)先聯立兩個函數解析式,再通過解方程求得交點B的坐標即可.
(3)作![]() 點關于
點關于![]() 軸的對稱點
軸的對稱點![]() ,可得
,可得![]() ,當
,當![]() 三點共線時,
三點共線時,![]() 有最大值;求出
有最大值;求出![]() 的解析式求解即可.
的解析式求解即可.
(1)過點![]() 作
作![]() 軸于
軸于![]() ,
,

![]() 的坐標為
的坐標為![]() ,
,![]() 的坐標為
的坐標為![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
故![]() ,
,
![]() ,
,
![]() 反比例函數表達式為:
反比例函數表達式為:![]() .
.
又![]() 點
點![]() 、
、![]() 在直線
在直線![]() 上,
上,
![]()
![]() ,解得:
,解得:![]() ,
,
![]() 一次函數的表達式為:
一次函數的表達式為:![]() ;
;
(2)由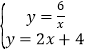 得:
得:![]() ,
,
解得:![]() 或
或![]() ,
,
![]() ,
,
![]() ;
;
(3)作![]() 點關于
點關于![]() 軸的對稱點
軸的對稱點![]() ,可得
,可得![]() ,
,
當![]() 三點構成三角形時,
三點構成三角形時,![]() ,
,
當![]() 三點共線時,
三點共線時,![]() ,
,
所以當![]() 三點共線時,
三點共線時,![]() 有最大值;
有最大值;
此時,由![]() 、
、![]() 可得
可得![]() 解析式為
解析式為![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 點坐標為
點坐標為![]() .
.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
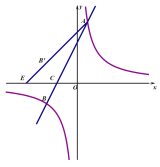
【題目】如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
(1)求證:AC是⊙O的切線;
(2)過點E作EH⊥AB,垂足為H,求證:CD=HF;
(3)若CD=1,EH=3,求BF及AF長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民節約用水,采用分段計費的方法按月計算每戶家庭的水費,月用水量不超過20![]() 時,按2元/
時,按2元/![]() 計費;月用水量超過20
計費;月用水量超過20![]() 時,其中的20
時,其中的20![]() 仍按2元/
仍按2元/![]() 收費,超過部分按
收費,超過部分按![]() 元/
元/![]() 計費.設每戶家庭用用水量為
計費.設每戶家庭用用水量為![]() 時,應交水費
時,應交水費![]() 元.
元.
(1)分別求出![]() 和
和![]() 時
時![]() 與
與![]() 的函數表達式;
的函數表達式;
(2)小明家第二季度交納水費的情況如下:
月份 | 四月份 | 五月份 | 六月份 |
交費金額 | 30元 | 34元 | 42.6元 |
小明家這個季度共用水多少立方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一張正方形紙的內部被針扎了2010個孔,這些孔和正方形的頂點之中的任何3點都不共線.作若干條互不相交的線段,它們的端點都是這些孔或正方形的頂點,這些線段將正方形分割成一些三角形,并且在這些三角形的內部和邊上都不再有小孔.請問一共作了多少條線段?共得到了多少個三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線 ![]() 經過
經過 ![]() ,
, ![]() 兩點,與
兩點,與 ![]() 軸相交于點
軸相交于點 ![]() ,連接
,連接 ![]() .點
.點 ![]() 為拋物線上一動點,過點
為拋物線上一動點,過點 ![]() 作
作 ![]() 軸的垂線
軸的垂線 ![]() ,交直線
,交直線 ![]() 于點
于點 ![]() ,交
,交 ![]() 軸于點
軸于點 ![]() .
.
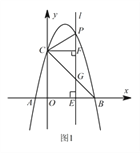
Ⅰ 求拋物線的表達式;
Ⅱ 當 ![]() 位于
位于 ![]() 軸右邊的拋物線上運動時,過點
軸右邊的拋物線上運動時,過點 ![]() 作
作 ![]() 直線
直線 ![]() ,
, ![]() 為垂足.當點
為垂足.當點 ![]() 運動到何處時,以
運動到何處時,以 ![]() ,
, ![]() ,
, ![]() 為頂點的三角形與
為頂點的三角形與 ![]() 相似?并求出此時點
相似?并求出此時點 ![]() 的坐標;
的坐標;
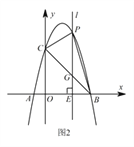
Ⅲ 如圖2,當點 ![]() 在位于直線
在位于直線 ![]() 上方的拋物線上運動時,連接
上方的拋物線上運動時,連接 ![]() ,
, ![]() .請問
.請問 ![]() 的面積
的面積 ![]() 能否取得最大值?若能,請求出最大面積
能否取得最大值?若能,請求出最大面積 ![]() ,并求出此時點
,并求出此時點 ![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并完成相應任務.
 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 折疊,使
折疊,使![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

任務:(1)試根據以上操作步驟證明![]() 就是
就是![]() 的黃金分割點;
的黃金分割點;
(2)請寫出一個生活中應用黃金分割的實際例子.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】港珠澳大橋,從2009年開工建造,于2018年10月24日正式通車.其全長55公里,連接港珠澳三地,集橋、島、隧于一體,是世界上最長的跨海大橋.如圖是港珠澳大橋的海豚塔部分效果圖,為了測得海豚塔斜拉索頂端A距離海平面的高度,先測出斜拉索底端C到橋塔的距離(CD的長)約為100米,又在C點測得A點的仰角為30°,測得B點的俯角為20°,求斜拉索頂端A點到海平面B點的距離(AB的長).(已知![]() ≈1.73,tan20°≈0.36,結果精確到0.1)
≈1.73,tan20°≈0.36,結果精確到0.1)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正多邊形每個內角比相鄰外角大60°.
(1)求這個正多邊形的邊數;
(2)求這個正多邊形的內切圓與外切圓的半徑之比;
(3)將這個多邊形對折,并完全重合,求得到圖形的內角和是多少度(按一層計算)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com