
 x2+mx+m+
x2+mx+m+ 的圖象與x軸相交于點(diǎn)A、B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸相交于點(diǎn)C,頂點(diǎn)D在第一象限.過點(diǎn)D作x軸的垂線,垂足為H.
的圖象與x軸相交于點(diǎn)A、B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸相交于點(diǎn)C,頂點(diǎn)D在第一象限.過點(diǎn)D作x軸的垂線,垂足為H. 時(shí),求tan∠ADH的值;
時(shí),求tan∠ADH的值;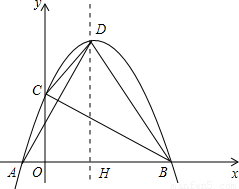
 代入y=-
代入y=- x2+mx+m+
x2+mx+m+ ,運(yùn)用配方法改寫成頂點(diǎn)式,求出頂點(diǎn)D,與x軸的交點(diǎn)A與B的坐標(biāo),得到DH,AH的長度,再根據(jù)正切函數(shù)的定義即可求出tan∠ADH的值;
,運(yùn)用配方法改寫成頂點(diǎn)式,求出頂點(diǎn)D,與x軸的交點(diǎn)A與B的坐標(biāo),得到DH,AH的長度,再根據(jù)正切函數(shù)的定義即可求出tan∠ADH的值; x2+mx+m+
x2+mx+m+ 運(yùn)用配方法改寫成頂點(diǎn)式,求出頂點(diǎn)D,與x軸的交點(diǎn)A與B的坐標(biāo),得到DH,AH的長度,再由拋物線的對(duì)稱性可知當(dāng)60°≤∠ADB≤90°時(shí),30°≤∠ADH≤45°,然后根據(jù)30°,45°角的正切函數(shù)值及銳角三角函數(shù)的增減性即可求出m的變化范圍;
運(yùn)用配方法改寫成頂點(diǎn)式,求出頂點(diǎn)D,與x軸的交點(diǎn)A與B的坐標(biāo),得到DH,AH的長度,再由拋物線的對(duì)稱性可知當(dāng)60°≤∠ADB≤90°時(shí),30°≤∠ADH≤45°,然后根據(jù)30°,45°角的正切函數(shù)值及銳角三角函數(shù)的增減性即可求出m的變化范圍; ),S△ABC=
),S△ABC= ×6×
×6× =
=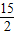 .設(shè)點(diǎn)D到直線BC的距離為d,根據(jù)S△DBC=
.設(shè)點(diǎn)D到直線BC的距離為d,根據(jù)S△DBC= BC•d=
BC•d=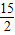 ,即可求出d的值.
,即可求出d的值.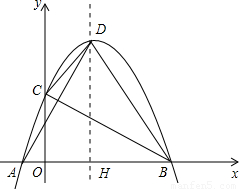 解:(1)∵當(dāng)m=
解:(1)∵當(dāng)m= 時(shí),y=-
時(shí),y=- x2+
x2+ x+2=-
x+2=- (x-
(x- )2+
)2+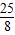 ,
, ,
,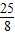 ),與x軸的交點(diǎn)A(-1,0),B(4,0),
),與x軸的交點(diǎn)A(-1,0),B(4,0),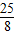 ,AH=
,AH= -(-1)=
-(-1)= ,
,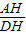 =
=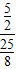 =
= ;
; x2+mx+m+
x2+mx+m+ =-
=- (x-m)2+
(x-m)2+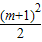 ,
,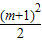 ),
), x2+mx+m+
x2+mx+m+ =0,解得:x=-1或2m+1
=0,解得:x=-1或2m+1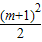 ,AH=m-(-1)=m+1,
,AH=m-(-1)=m+1,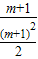 =
=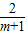 .
.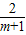 =
=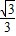 ,
,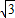 -1,
-1,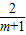 =1,
=1,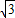 -1;
-1;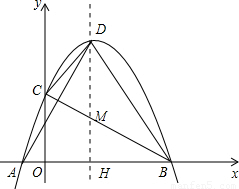 (3)設(shè)DH與BC交于點(diǎn)M,則點(diǎn)M的橫坐標(biāo)為m.
(3)設(shè)DH與BC交于點(diǎn)M,則點(diǎn)M的橫坐標(biāo)為m. )的直線解析式為;y=kx+b,
)的直線解析式為;y=kx+b,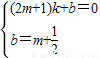 ,
,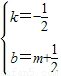 ,
, x+m+
x+m+ .
. m+m+
m+m+ =
=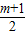 ,
,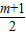 ).
).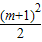 -
-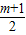 =
=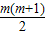 ,AB=(2m+1)-(-1)=2m+2,
,AB=(2m+1)-(-1)=2m+2,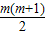 •(2m+1)=(2m+2)•(m+
•(2m+1)=(2m+2)•(m+ ),
), ),
),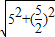 =
=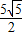 ,
, ×6×
×6× =
=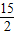 .
. BC•d,
BC•d, ×
×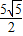 •d=
•d=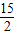 ,
,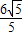 .
.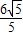 .
. DM•OB,從而根據(jù)S△DBC=S△ABC求出m的值是解題的關(guān)鍵.
DM•OB,從而根據(jù)S△DBC=S△ABC求出m的值是解題的關(guān)鍵. 


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
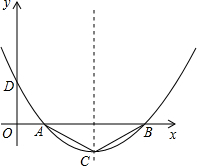 如圖,二次函數(shù)的圖象經(jīng)過點(diǎn)D(0,
如圖,二次函數(shù)的圖象經(jīng)過點(diǎn)D(0,| 7 |
| 9 |
| 3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于B、C兩點(diǎn),與y軸交于點(diǎn)A(0,-3),∠ABC=45°,∠ACB=60°,求這個(gè)二次函數(shù)解析式.
如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于B、C兩點(diǎn),與y軸交于點(diǎn)A(0,-3),∠ABC=45°,∠ACB=60°,求這個(gè)二次函數(shù)解析式.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 某公司推出了一種高效環(huán)保型洗滌用品,年初上市后,公司經(jīng)歷了從虧損到盈利的過程,如圖的二次函數(shù)圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時(shí)間t(月)之間的關(guān)系(即前t個(gè)月的利潤總和s與t之間的關(guān)系).根據(jù)圖象提供的信息,解答下列問題:
某公司推出了一種高效環(huán)保型洗滌用品,年初上市后,公司經(jīng)歷了從虧損到盈利的過程,如圖的二次函數(shù)圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時(shí)間t(月)之間的關(guān)系(即前t個(gè)月的利潤總和s與t之間的關(guān)系).根據(jù)圖象提供的信息,解答下列問題:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸相交于兩個(gè)點(diǎn),根據(jù)圖象回答:(1)b
如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸相交于兩個(gè)點(diǎn),根據(jù)圖象回答:(1)b查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com