激情小说综合网,日韩av在线不卡,丁香六月av

【題目】如圖，將Rt△ABC繞直角頂點C順時針旋轉90°，得到△A′B′C，連接AA′，若∠1=20°，則∠B的度數是（）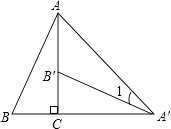
A.70°
B.65°
C.60°
D.55°

【答案】B
【解析】解：∵Rt△ABC繞直角頂點C順時針旋轉90°得到△A′B′C， ∴AC=A′C，
∴△ACA′是等腰直角三角形，
∴∠CAA′=45°，
∴∠A′B′C=∠1+∠CAA′=20°+45°=65°，
由旋轉的性質得∠B=∠A′B′C=65°．
故選：B．
根據旋轉的性質可得AC=A′C，然后判斷出△ACA′是等腰直角三角形，根據等腰直角三角形的性質可得∠CAA′=45°，再根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠A′B′C，然后根據旋轉的性質可得∠B=∠A′B′C．

練習冊系列答案

課課練與單元測試系列答案

世紀金榜小博士單元期末一卷通系列答案

單元測試AB卷臺海出版社系列答案

黃岡新思維培優考王單元加期末卷系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】小明在做課本“目標與評定”中的一道題：如圖1，直線a，b所成的角跑到畫板外面去了，你有什么辦法量出這兩條直線所成的角的度數？小明的做法是：如圖2，畫PC∥a，量出直線b與PC的夾角度數，即直線a，b所成角的度數．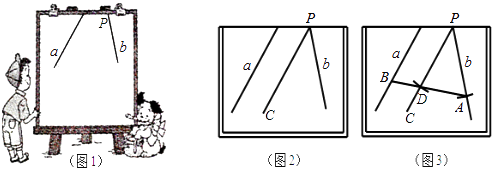
（1）請寫出這種做法的理由；
（2）小明在此基礎上又進行了如下操作和探究（如圖3）：①以P為圓心，任意長為半徑畫圓弧，分別交直線b，PC于點A，D；②連結AD并延長交直線a于點B，請寫出圖3中所有與∠PAB相等的角，并說明理由；
（3）請在圖3畫板內作出“直線a，b所成的跑到畫板外面去的角”的平分線（畫板內的部分），只要求作出圖形，并保留作圖痕跡．

查看答案和解析>>

科目：初中數學 來源： 題型：

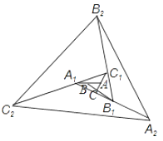
【題目】如圖，△ABC面積為1，第一次操作：分別延長AB，BC，CA至點A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA，順次連接A1,B1,C1,得到△A1B1C1.第二次操作：分別延長A1B1,B1C1、C1A1至點A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1 ,順次連接A2,B2,C2,得到△A2B2C2,…按此規律，經過2015次操作后△A2015B2015C2015的面積為________．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】四邊形ABCD是直角梯形，AB∥CD，AB⊥BC，且BC=CD=2，AB=3，把梯形ABCD分別繞直線AB，CD旋轉一周，所得幾何體的表面積分別為S1 ， S2 ，則|S1﹣S2|=（平方單位）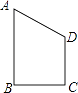

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖所示,某公司有三個住宅區可看作一點,A,B,C各區分別住有職工30人、15人、10人,且這三個住宅區在一條大道上(A,B,C三點共線),已知AB=100米,BC=200米.為了方便職工上下班,該公司的接送車打算在此間只設一個停靠點,為使所有的人步行到停靠點的路程之和最小,那么該停靠點的位置應設在( 　)

A. 點A B. 點B

C. A,B之間 D. B,C之間

查看答案和解析>>

科目：初中數學 來源： 題型：

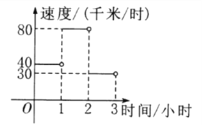
【題目】某人駕車從鄉村進城.各時間段的行駛速度如圖所示.當時，其行駛路程與時間之間的函數表達式是________，當時，其行駛路程與時間之間的函數表達式是________，當時，其行駛路程與時間之間的函數表達式是________.

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，矩形OABC的頂點A、C分別在x、y軸的正半軸上，點D為對角線OB的中點，點E（4，n）在邊AB上，反比例函數（k≠0）在第一象限內的圖象經過點D、E，且tan∠BOA= ．

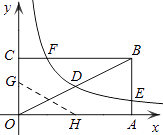
（1）求邊AB的長；
（2）求反比例函數的解析式和n的值；
（3）若反比例函數的圖象與矩形的邊BC交于點F，將矩形折疊，使點O與點F重合，折痕分別與x、y軸正半軸交于點H、G，求線段OG的長．