
已知:如圖,⊙P與x軸相切于坐標原點O,點A(0,2)是⊙P與y軸的交點,點B(-2![]() ,0)在x軸上.連結BP交⊙P于點C,連結AC并延長交x軸于點D.
,0)在x軸上.連結BP交⊙P于點C,連結AC并延長交x軸于點D.
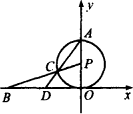
(1)求線段BC的長;
(2)求直線AC的關系式;
(3)當點B在x軸上移動時,是否存在點B,使△BOP相似于△AOD?若存在,求出符合條件的點的坐標;若不存在,請說明理由.
|
解:(1)由題意,得OP=1,BO=2 在Rt△BOP中, ∵BP2=OP2+BO2,∴(BC+1)2=12+(2 ∴BC=2; (2)過點C作CE⊥x軸于E,CF⊥y軸于F, 在△PBO中,∵CF∥BO,∴ 即 同理可求得CE= 因此C(- 把A(0,2),C(- ∴所求函數關系式為y= (3)在x軸上存在點B,使△BOP與△AOD相似. ∵∠OPB>∠OAD,∴∠OPB≠∠OAB 故若要△BOP與△AOD相似, 則∠OBP=∠OAD.又∠OPB=2∠OAD, ∴∠OPB=2∠OBP ∵∠OPB+∠OBP=90°,∴3∠OBP=90°, ∴∠OBP=30°. 因此OB=cot30°·OP= ∴B1點坐標為(- 根據對稱性可求得符合條件的B2坐標( 綜上,符合條件的B點坐標有兩個:B1(- |


 步步高達標卷系列答案
步步高達標卷系列答案科目:初中數學 來源: 題型:
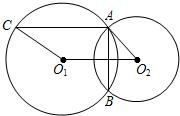
 21、已知:如圖,⊙O1與⊙O2相交于A、B兩點,過A的直線交⊙O1于C,交⊙O2于D,過B的直線交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如圖,⊙O1與⊙O2相交于A、B兩點,過A的直線交⊙O1于C,交⊙O2于D,過B的直線交⊙O1于E,交⊙O2于F,且CD∥EF.查看答案和解析>>
科目:初中數學 來源: 題型:
 ,⊙O2的半徑為
,⊙O2的半徑為| 13 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (1997•南京)已知:如圖,⊙O1與⊙O2外切于點P,A為⊙O1上一點,直線AC切⊙O2于點C,且交⊙O1于點B,AP的延長線交⊙O2于點D.
(1997•南京)已知:如圖,⊙O1與⊙O2外切于點P,A為⊙O1上一點,直線AC切⊙O2于點C,且交⊙O1于點B,AP的延長線交⊙O2于點D.| 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com