
【題目】(1)已知矩形A的長、寬分別是2和1,那么是否存在另一個矩形B,它的周長和面積分別是矩形A的周長和面積的2倍?對上述問題,小明同學從“圖形”的角度,利用函數圖象給予了解決.小明論證的過程開始是這樣的:如果用x、y分別表示矩形的長和寬,那么矩形B滿足x+y=6,xy=4.請你按照小明的論證思路完成后面的論證過程.(畫圖并簡單的文字說明)
(2)已知矩形A的長和寬分別是2和1,那么是否存在一個矩形C,它的周長和面積分別是矩形A的周長和面積的一半?小明認為這個問題是肯定的,你同意小明的觀點嗎?為什么?(同上要求)
【答案】(1)答案見解析;(2)不同意,理由見解析
【解析】試題分析:(1)、將點同時滿足要求的點(x,y)看作一次函數y=-x+6的圖象與反比例函數y=![]() 的圖象在第一象限內交點的坐標,如果有交點就是成立;(2)、分別畫出一次函數y=-x+
的圖象在第一象限內交點的坐標,如果有交點就是成立;(2)、分別畫出一次函數y=-x+![]() 的圖象與反比例函數y=
的圖象與反比例函數y=![]() 的圖象,然后看他們在第一象限是否有交點.
的圖象,然后看他們在第一象限是否有交點.
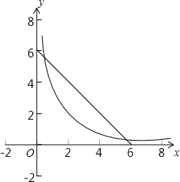
試題解析:(1)、點(x,y)可以看作一次函數y=-x+6的圖象在第一象限內點的坐標,
點(x,y)又可以看作反比例函數y=![]() 的圖象在第一象限內點的坐標,
的圖象在第一象限內點的坐標,
而滿足問題要求的點(x,y)就可以看作一次函數y=-x+6的圖象與反比例函數y=![]() 的圖象在第一象限內交點的坐標.
的圖象在第一象限內交點的坐標.
分別畫出兩圖象(如右圖),從圖中可看出,這樣的交點存在,即滿足要求的矩形B存在.
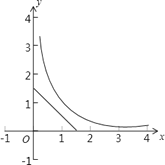
(2)、不同意小明的觀點.如果用x,y分別表示矩形的長和寬,那么矩形C滿足x+y=![]() ,xy=1,
,xy=1,
滿足要求的(x,y)可以看作一次函數y=-x+![]() 的圖象與反比例函數y=
的圖象與反比例函數y=![]() 的圖象在第一象限內交點的坐標.
的圖象在第一象限內交點的坐標.
畫圖(如右圖)可看出,這樣的交點不存在,即滿足要求的矩形C是不存在的.所以不同意小明的觀點.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AD=5,點E、F是正方形ABCD內的兩點,且AE=FC=4,BE=DF=3,則以EF為直徑的圓的面積為( )
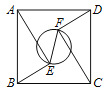
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年5月18日華中旅游博覽會在漢召開.開幕式上用到甲、乙、丙三種造型的花束,甲種花束由3朵紅花、2朵黃花和1朵紫花搭配而成,乙種花束由2朵紅花和2朵黃花搭配而成,丙種花束由2朵紅花、1朵黃花和1朵紫花搭配而成.這些花束一共用了580朵紅花,150朵紫花,則黃花一共用了 朵.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=90°,AC=AB,點D為直線BC上的一動點,以AD為邊作△ADE(頂點A、D、E按逆時針方向排列),且∠DAE=90°,AD=AE,連接CE.
⑴ 如圖1,若點D在BC邊上(點D與B、C不重合),求∠BCE的度數.
⑵ 如圖2,若點D在CB的延長線上,若DB=5,BC=7,求△ADE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一方有難八方支援,某市政府籌集了抗旱必需物資120噸打算運往災區,現有甲、乙、丙三種車型供選擇,每輛車的運載能力和運費如下表所示:(假設每輛車均滿載)
車型 | 甲 | 乙 | 丙 |
汽車運載量(噸/輛) | 5 | 8 | 10 |
汽車運費(元/輛) | 400 | 500 | 600 |
(1)若全部物資都用甲、乙兩種車型來運送,需運費8200元,問分別需甲、乙兩種車型各幾輛?
(2)為了節約運費,該市政府可以調用甲、乙、丙三種車型參與運送,已知它們的總輛數為16輛,你能通過列方程組的方法分別求出幾種車型的輛數嗎?
(3)求出那種方案的運費最省?最省是多少元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com