【題目】在美化校園的活動中，某興趣小組想借助如圖所示的直角墻角（兩邊足夠長），用28m長的籬笆圍成一個矩形花園ABCD（籬笆只圍AB，BC兩邊），設AB=xm.
（1）若花園的面積為192m2, 求x的值；
（2）若在P處有一棵樹與墻CD，AD的距離分別是15m和6m，要將這棵樹圍在花園內（含邊界，不考慮樹的粗細），求花園面積S的最大值.
【答案】（1）12m或16m；（2）195.
【解析】
試題(1)、根據AB=x可得BC=28－x，然后根據面積列出一元二次方程求出x的值；(2)、根據題意列出S和x的函數關系熟，然后根據題意求出x的取值范圍，然后根據函數的性質求出最大值.
試題解析：(1)、∵AB=xm，則BC=（28﹣x）m， ∴x（28﹣x）=187，
解得：x1=11，x2=17， 答：x的值為11m或17m
(2)、∵AB=xm， ∴BC=28﹣x， ∴S=x（28﹣x）=﹣x2+28x=﹣（x﹣14）2+196，
∵在P處有一棵樹與墻CD，AD的距離分別是16m和6m，
∵28-x≥16,x≥6 ∴6≤x≤12，
∴當x=12時，S取到最大值為：S=﹣（12﹣14）2+196=192，
答：花園面積S的最大值為192平方米．
名校課堂系列答案科目：初中數學 來源： 題型：
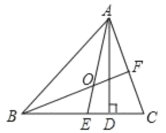
【題目】(1)如圖，在
中，
是高，
是角平分線，它們相交于點
，
．求
和
的度數．
(2)一個多邊形的內角和是外角和的3倍，它是幾邊形?若這個多邊形的各個內角都相等，求這個多邊形的每個內角的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，反比例函數y= 
的圖象與一次函數y=x+b的圖象交
于點A（1，4）、點B（-4，n）．
（1）求一次函數和反比例函數的解析式；
（2）求△OAB的面積；
（3）直接寫出一次函數值大于反比例函數值的自變量x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在“愛我永州”中學生演講比賽中，五位評委分別給甲、乙兩位選手的評分如下：
甲：8、7、9、8、8
乙：7、9、6、9、9
則下列說法中錯誤的是（ ）
A．甲、乙得分的平均數都是8
B．甲得分的眾數是8，乙得分的眾數是9
C．甲得分的中位數是9，乙得分的中位數是6
D．甲得分的方差比乙得分的方差小
查看答案和解析>>
科目：初中數學 來源： 題型：
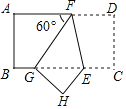
【題目】如圖，在矩形ABCD中，點F在AD上，點E在BC上，把這個矩形沿EF折疊后，使點D恰好落在BC邊上的G點處，若矩形面積為
且
，GE=2BG，則折痕EF的長為（ ）
A. 4 B. 
C. 2 D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在五張正面分別寫有數字﹣2，﹣1，0，1，2的卡片，它們的背面完全相同，現將這五張卡片背面朝上洗勻．
（1）從中任意抽取一張卡片，則所抽卡片上數字的絕對值不大于1的概率是 ；
（2）先從中任意抽取一張卡片，以其正面數字作為a的值，然后再從剩余的卡片隨機抽一張，以其正面的數字作為b的值，請用列表法或畫樹狀圖法，求點Q（a，b）在第二象限的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
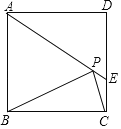
【題目】如圖，在正方形ABCD中，AD=2
，把邊BC繞點B逆時針旋轉30°得到線段BP，連接AP并延長交CD于點E，連接PC，則三角形PCE的面積為___．
查看答案和解析>>
科目：初中數學 來源： 題型：
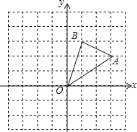
【題目】如圖，在邊長為
的正方形組成的網格中，
的頂點均在格點上，點
、
的坐標分別是
，
，關于
軸對稱的圖形為
．
畫出并寫出點
的坐標為________；
寫出的面積為________；
點
在
軸上，使
的值最小，寫出點的坐標為________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
