

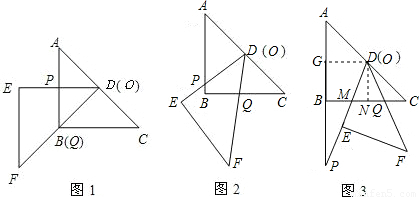
 解:(1)∵∠A=∠C=45°,∠APD=∠QDC=90°,
解:(1)∵∠A=∠C=45°,∠APD=∠QDC=90°,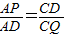 .
. AC)2=8.
AC)2=8.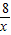
 AB•BC-
AB•BC- CQ•DN-
CQ•DN- AP•DG
AP•DG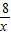 (2<x<4)
(2<x<4)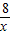 ,PB=
,PB=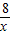 -4,易證:△PBM∽△DNM,
-4,易證:△PBM∽△DNM,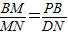 即
即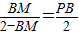 解得
解得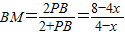 .
.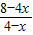 .
. MQ•DN=4-x-
MQ•DN=4-x-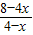 (0<x≤2).
(0<x≤2).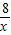 .
.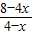 (或y=
(或y=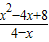 ).
).

 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源:2009年山東省濟南市省實驗中學中考數學測試試卷(2)(解析版) 題型:解答題
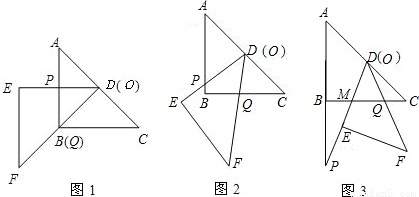
查看答案和解析>>
科目:初中數學 來源:2009年高中段自主招生科學素養模擬卷(數學部分)(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2006年湖南省常德市中考數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2006年湖南省常德市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com