

 ,tan37°=
,tan37°= )
)
 =3;
=3; ×3×4×4=24(dm3);
×3×4×4=24(dm3); ,
, (x+y)×4×4=24,
(x+y)×4×4=24, ;
; PB•BB′×4=24,得PB=3,
PB•BB′×4=24,得PB=3, ,得∠PB′B=37°.
,得∠PB′B=37°. .
. <MN.
<MN. ×
× ×1+
×1+ (4﹣2
(4﹣2 +4)×2=8﹣
+4)×2=8﹣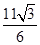 .
.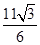 )=
)=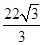 ﹣8>4(dm3).
﹣8>4(dm3). .
.

科目:初中數學 來源:不詳 題型:解答題
 ≌
≌ .
. 向左平移,使
向左平移,使 與
與 重合,得
重合,得 ,
, 交
交 于點
于點 .請判斷AH與ED的位置關系,并說明理由.
.請判斷AH與ED的位置關系,并說明理由. 的長.
的長.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
 ,一邊長是4cm,那么對角線長是___ ____;已知菱形兩條對角線的長分別為5cm和8cm,則這個菱形的面積是______cm
,一邊長是4cm,那么對角線長是___ ____;已知菱形兩條對角線的長分別為5cm和8cm,則這個菱形的面積是______cm .
.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 中,點A的坐標是(-2,1),點C的縱坐標是4,則B、C兩點的坐標為( )
中,點A的坐標是(-2,1),點C的縱坐標是4,則B、C兩點的坐標為( )
 ,
, )、(
)、( ,
, ) B.(
) B.( ,
, )、(
)、( ,
, )
) ,
, )、(
)、( ,
, ) D.(
) D.( ,
, ) 、(
) 、( ,
, )
)查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.AB=CD AB ∥CD | B.∠A=∠C∠B=∠D |
| C.AB=AD BC=CD | D.AB=CD AD=BC |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com